This PR adds support for `SymInt`s in python. Namely,
* `THPVariable_size` now returns `sym_sizes()`
* python arg parser is modified to parse PyObjects into ints and `SymbolicIntNode`s
* pybind11 bindings for `SymbolicIntNode` are added, so size expressions can be traced
* a large number of tests added to demonstrate how to implement python symints.
Pull Request resolved: https://github.com/pytorch/pytorch/pull/78135
Approved by: https://github.com/ezyang
This PR heavily simplifies the code of `linalg.solve`. At the same time,
this implementation saves quite a few copies of the input data in some
cases (e.g. A is contiguous)
We also implement it in such a way that the derivative goes from
computing two LU decompositions and two LU solves to no LU
decompositions and one LU solves. It also avoids a number of unnecessary
copies the derivative was unnecessarily performing (at least the copy of
two matrices).
On top of this, we add a `left` kw-only arg that allows the user to
solve `XA = B` rather concisely.
Pull Request resolved: https://github.com/pytorch/pytorch/pull/74046
Approved by: https://github.com/nikitaved, https://github.com/IvanYashchuk, https://github.com/mruberry
This PR adds `linalg.lu_solve`. While doing so, I found a bug in MAGMA
when calling the batched MAGMA backend with trans=True. We work around
that by solving the system solving two triangular systems.
We also update the heuristics for this function, as they were fairly
updated. We found that cuSolver is king, so luckily we do not need to
rely on the buggy backend from magma for this function.
We added tests testing this function left and right. We also added tests
for the different backends. We also activated the tests for AMD, as
those should work as well.
Fixes https://github.com/pytorch/pytorch/issues/61657
Pull Request resolved: https://github.com/pytorch/pytorch/pull/77634
Approved by: https://github.com/malfet
```Python
chebyshev_polynomial_v(input, n, *, out=None) -> Tensor
```
Chebyshev polynomial of the third kind $V_{n}(\text{input})$.
```Python
chebyshev_polynomial_w(input, n, *, out=None) -> Tensor
```
Chebyshev polynomial of the fourth kind $W_{n}(\text{input})$.
```Python
legendre_polynomial_p(input, n, *, out=None) -> Tensor
```
Legendre polynomial $P_{n}(\text{input})$.
```Python
shifted_chebyshev_polynomial_t(input, n, *, out=None) -> Tensor
```
Shifted Chebyshev polynomial of the first kind $T_{n}^{\ast}(\text{input})$.
```Python
shifted_chebyshev_polynomial_u(input, n, *, out=None) -> Tensor
```
Shifted Chebyshev polynomial of the second kind $U_{n}^{\ast}(\text{input})$.
```Python
shifted_chebyshev_polynomial_v(input, n, *, out=None) -> Tensor
```
Shifted Chebyshev polynomial of the third kind $V_{n}^{\ast}(\text{input})$.
```Python
shifted_chebyshev_polynomial_w(input, n, *, out=None) -> Tensor
```
Shifted Chebyshev polynomial of the fourth kind $W_{n}^{\ast}(\text{input})$.
Pull Request resolved: https://github.com/pytorch/pytorch/pull/78304
Approved by: https://github.com/mruberry
Adds:
```Python
bessel_j0(input, *, out=None) -> Tensor
```
Bessel function of the first kind of order $0$, $J_{0}(\text{input})$.
```Python
bessel_j1(input, *, out=None) -> Tensor
```
Bessel function of the first kind of order $1$, $J_{1}(\text{input})$.
```Python
bessel_j0(input, *, out=None) -> Tensor
```
Bessel function of the second kind of order $0$, $Y_{0}(\text{input})$.
```Python
bessel_j1(input, *, out=None) -> Tensor
```
Bessel function of the second kind of order $1$, $Y_{1}(\text{input})$.
```Python
modified_bessel_i0(input, *, out=None) -> Tensor
```
Modified Bessel function of the first kind of order $0$, $I_{0}(\text{input})$.
```Python
modified_bessel_i1(input, *, out=None) -> Tensor
```
Modified Bessel function of the first kind of order $1$, $I_{1}(\text{input})$.
```Python
modified_bessel_k0(input, *, out=None) -> Tensor
```
Modified Bessel function of the second kind of order $0$, $K_{0}(\text{input})$.
```Python
modified_bessel_k1(input, *, out=None) -> Tensor
```
Modified Bessel function of the second kind of order $1$, $K_{1}(\text{input})$.
Pull Request resolved: https://github.com/pytorch/pytorch/pull/78451
Approved by: https://github.com/mruberry
Adds:
```Python
chebyshev_polynomial_t(input, n, *, out=None) -> Tensor
```
Chebyshev polynomial of the first kind $T_{n}(\text{input})$.
If $n = 0$, $1$ is returned. If $n = 1$, $\text{input}$ is returned. If $n < 6$ or $|\text{input}| > 1$ the recursion:
$$T_{n + 1}(\text{input}) = 2 \times \text{input} \times T_{n}(\text{input}) - T_{n - 1}(\text{input})$$
is evaluated. Otherwise, the explicit trigonometric formula:
$$T_{n}(\text{input}) = \text{cos}(n \times \text{arccos}(x))$$
is evaluated.
## Derivatives
Recommended $k$-derivative formula with respect to $\text{input}$:
$$2^{-1 + k} \times n \times \Gamma(k) \times C_{-k + n}^{k}(\text{input})$$
where $C$ is the Gegenbauer polynomial.
Recommended $k$-derivative formula with respect to $\text{n}$:
$$\text{arccos}(\text{input})^{k} \times \text{cos}(\frac{k \times \pi}{2} + n \times \text{arccos}(\text{input})).$$
## Example
```Python
x = torch.linspace(-1, 1, 256)
matplotlib.pyplot.plot(x, torch.special.chebyshev_polynomial_t(x, 10))
```
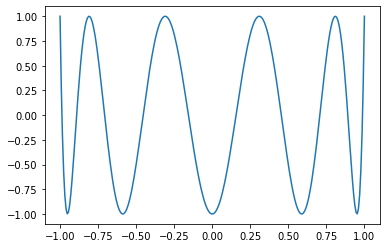
Pull Request resolved: https://github.com/pytorch/pytorch/pull/78196
Approved by: https://github.com/mruberry
Euler beta function:
```Python
torch.special.beta(input, other, *, out=None) → Tensor
```
`reentrant_gamma` and `reentrant_ln_gamma` implementations (using Stirling’s approximation) are provided. I started working on this before I realized we were missing a gamma implementation (despite providing incomplete gamma implementations). Uses the coefficients computed by Steve Moshier to replicate SciPy’s implementation. Likewise, it mimics SciPy’s behavior (instead of the behavior in Cephes).
Pull Request resolved: https://github.com/pytorch/pytorch/pull/78031
Approved by: https://github.com/mruberry
We don't have any coverage for meta tensor correctness for backwards
because torch function mode can only allow us to interpose on
Python torch API calls, but backwards invocations happen from C++.
To make this possible, I add torch_dispatch_meta test which runs the
tests with __torch_dispatch__
While doing this, I needed to generate fresh expected failure / skip
lists for the new test suite, and I discovered that my original
scaffolding for this purpose was woefully insufficient. So I rewrote
how the test framework worked, and at the same time rewrote the
__torch_function__ code to also use the new logic. Here's whats
new:
- Expected failure / skip is now done on a per function call basis,
rather than the entire test. This means that separate OpInfo
samples for a function don't affect each other.
- There are now only two lists: expect failure list (where the test
consistently fails on all runs) and skip list (where the test
sometimes passes and fails.
- We explicitly notate the dtype that failed. I considered detecting
when something failed on all dtypes, but this was complicated and
listing everything out seemed to be nice and simple. To keep the
dtypes short, I introduce a shorthand notation for dtypes.
- Conversion to meta tensors is factored into its own class
MetaConverter
- To regenerate the expected failure / skip lists, just run with
PYTORCH_COLLECT_EXPECT and filter on a specific test type
(test_meta or test_dispatch_meta) for whichever you want to update.
Other misc fixes:
- Fix max_pool1d to work with BFloat16 in all circumstances, by making
it dispatch and then fixing a minor compile error (constexpr doesn't
work with BFloat16)
- Add resolve_name for turning random torch API functions into string
names
- Add push classmethod to the Mode classes, so that you can more easily
push a mode onto the mode stack
- Add some more skips for missing LAPACK
- Added an API to let you query if there's already a registration for
a function, added a test to check that we register_meta for all
decompositions (except detach, that decomp is wrong lol), and then
update all the necessary sites to make the test pass.
Signed-off-by: Edward Z. Yang <ezyangfb.com>
Pull Request resolved: https://github.com/pytorch/pytorch/pull/77477
Approved by: https://github.com/zou3519
This PR adds `linalg.vander`, the linalg version of `torch.vander`.
We add autograd support and support for batched inputs.
We also take this chance to improve the docs (TODO: Check that they
render correctly!) and add an OpInfo.
**Discussion**: The current default for the `increasing` kwargs is extremely
odd as it is the opposite of the classical definition (see
[wiki](https://en.wikipedia.org/wiki/Vandermonde_matrix)). This is
reflected in the docs, where I explicit both the odd defaults that we
use and the classical definition. See also [this stackoverflow
post](https://stackoverflow.com/a/71758047/5280578), which shows how
people are confused by this defaults.
My take on this would be to correct the default to be `increasing=True`
and document the divergence with NumPy (as we do for other `linalg`
functions) as:
- It is what people expect
- It gives the correct determinant called "the Vandermonde determinant" rather than (-1)^{n-1} times the Vandermonde det (ugh).
- [Minor] It is more efficient (no `flip` needed)
- Since it's under `linalg.vander`, it's strictly not a drop-in replacement for `np.vander`.
We will deprecate `torch.vander` in a PR after this one in this stack
(once we settle on what's the correct default).
Thoughts? mruberry
cc kgryte rgommers as they might have some context for the defaults of
NumPy.
Fixes https://github.com/pytorch/pytorch/issues/60197
Pull Request resolved: https://github.com/pytorch/pytorch/pull/76303
Approved by: https://github.com/albanD, https://github.com/mruberry