Chebyshev polynomial of the second kind (#78293)

Adds:

```Python
chebyshev_polynomial_u(input, n, *, out=None) -> Tensor
```

Chebyshev polynomial of the second kind $U_{n}(\text{input})$.

If $n = 0$, $1$ is returned. If $n = 1$, $2 \times \text{input}$ is returned. If $n < 6$ or $|\text{input}| > 1$ the recursion:

$$T_{n + 1}(\text{input}) = 2 \times \text{input} \times T_{n}(\text{input}) - T_{n - 1}(\text{input})$$

is evaluated. Otherwise, the explicit trigonometric formula:

$$\frac{\text{sin}((n + 1) \times \text{arccos}(\text{input}))}{\text{sin}(\text{arccos}(\text{input}))}$$

is evaluated.

## Derivatives

Recommended first derivative formula with respect to $\text{input}$:

$$\frac{(-1 - n)\times U_{-1 + n}(\text{input}) + n \times \text{input} \times U_{n}(x)}{-1 + \text{input}^{2}}.$$

Recommended $k$-derivative formula with respect to $\text{n}$:

$$\frac{\text{arccos}(\text{input})^{k} \times \text{sin}(\frac{k \times \pi}{2} + (1 + n) \times \text{arccos}(\text{input}))}{\sqrt{1 - \text{input}^{2}}}.$$

## Example

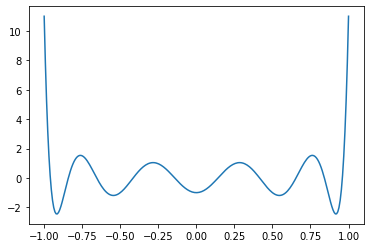
```Python
x = torch.linspace(-1.0, 1.0, 256)

matplotlib.pyplot.plot(x, torch.special.chebyshev_polynomial_u(x, 10))
```

![image](https://user-images.githubusercontent.com/315821/170352780-12af63d3-ce31-4948-8b68-8ecc37c71ac5.png)

Pull Request resolved: https://github.com/pytorch/pytorch/pull/78293
Approved by: https://github.com/mruberry

aten/src/ATen/native/BinaryOps.cpp

@@ -94,6 +94,10 @@ TORCH_META_FUNC(special_chebyshev_polynomial_t) (const Tensor& self, const Tenso
   build_borrowing_binary_float_op(maybe_get_output(), self, n);
 }
 
+TORCH_META_FUNC(special_chebyshev_polynomial_u) (const Tensor& self, const Tensor& n) {
+  build_borrowing_binary_float_op(maybe_get_output(), self, n);
+}
+
 TORCH_META_FUNC2(copysign, Tensor) (
   const Tensor& self, const Tensor& other
 ) {
@@ -281,6 +285,7 @@ DEFINE_DISPATCH(xlogy_stub);
 DEFINE_DISPATCH(xlog1py_stub);
 DEFINE_DISPATCH(zeta_stub);
 DEFINE_DISPATCH(chebyshev_polynomial_t_stub);
+DEFINE_DISPATCH(chebyshev_polynomial_u_stub);
 
 TORCH_IMPL_FUNC(sub_out) (
   const Tensor& self, const Tensor& other, const Scalar& alpha, const Tensor& result
@@ -331,6 +336,10 @@ TORCH_IMPL_FUNC(special_chebyshev_polynomial_t_out) (const Tensor& self, const T
   chebyshev_polynomial_t_stub(device_type(), *this);
 }
 
+TORCH_IMPL_FUNC(special_chebyshev_polynomial_u_out) (const Tensor& self, const Tensor& n, const Tensor& result) {
+  chebyshev_polynomial_u_stub(device_type(), *this);
+}
+
 TORCH_IMPL_FUNC(tanh_backward_out) (const Tensor& grad_output, const Tensor& output, const Tensor& result) {
   tanh_backward_stub(device_type(), *this);
 }
@@ -407,6 +416,22 @@ Tensor& special_chebyshev_polynomial_t_out(const Tensor& self, const Scalar& n,
   return at::special_chebyshev_polynomial_t_out(result, self, wrapped_scalar_tensor(n));
 }
 
+Tensor special_chebyshev_polynomial_u(const Scalar& x, const Tensor& n) {
+  return at::special_chebyshev_polynomial_u(wrapped_scalar_tensor(x), n);
+}
+
+Tensor special_chebyshev_polynomial_u(const Tensor& x, const Scalar& n) {
+  return at::special_chebyshev_polynomial_u(x, wrapped_scalar_tensor(n));
+}
+
+Tensor& special_chebyshev_polynomial_u_out(const Scalar& self, const Tensor& n, Tensor& result) {
+  return at::special_chebyshev_polynomial_u_out(result, wrapped_scalar_tensor(self), n);
+}
+
+Tensor& special_chebyshev_polynomial_u_out(const Tensor& self, const Scalar& n, Tensor& result) {
+  return at::special_chebyshev_polynomial_u_out(result, self, wrapped_scalar_tensor(n));
+}
+
 Tensor& special_gammainc_out(const Tensor& self, const Tensor& other, Tensor& result) {
   return at::igamma_out(result, self, other);
 }

aten/src/ATen/native/BinaryOps.h

@@ -102,5 +102,6 @@ DECLARE_DISPATCH(structured_binary_fn, xlogy_stub);
 DECLARE_DISPATCH(structured_binary_fn, xlog1py_stub);
 DECLARE_DISPATCH(structured_binary_fn, zeta_stub);
 DECLARE_DISPATCH(structured_binary_fn, chebyshev_polynomial_t_stub);
+DECLARE_DISPATCH(structured_binary_fn, chebyshev_polynomial_u_stub);
 
 }} // namespace at::native

aten/src/ATen/native/Math.h

@@ -2214,11 +2214,59 @@ static inline C10_HOST_DEVICE T chebyshev_polynomial_t_forward(T x, std::int64_t
     }
 
     return r;
-}
+} // chebyshev_polynomial_t_forward(T x, std::int64_t n)
 
 template<typename T, bool is_cuda=false>
 static inline C10_HOST_DEVICE T chebyshev_polynomial_t_forward(T x, T n) {
     return chebyshev_polynomial_t_forward(x, static_cast<std::int64_t>(n));
-}
+} // chebyshev_polynomial_t_forward(T x, T n)
+
+template<typename T>
+static inline C10_HOST_DEVICE T chebyshev_polynomial_u_forward(T x, std::int64_t n) {
+    if (n < 0) {
+        return T(0.0);
+    }
+
+    if (std::abs(x) == T(1.0)) {
+        if (x > T(0.0) || n % 2 == 0) {
+            return n + 1;
+        }
+
+        return -(n + 1);
+    }
+
+    if ((n > 8) && (std::abs(x) < T(1.0))) {
+        if (std::sin(std::acos(x)) != T(0.0)) {
+            return std::sin((n + 1) * std::acos(x)) / std::sin(std::acos(x));
+        }
+
+        return (n + 1) * std::cos((n + 1) * std::acos(x)) / x;
+    }
+
+    if (n == 0) {
+        return T(1.0);
+    }
+
+    if (n == 1) {
+        return x + x;
+    }
+
+    T p = T(1.0);
+    T q = x + x;
+    T r;
+
+    for (int64_t k = 2; k <= n; k++) {
+        r = (x + x) * q - p;
+        p = q;
+        q = r;
+    }
+
+    return r;
+} // chebyshev_polynomial_u_forward(T x, std::int64_t n)
+
+template<typename T, bool is_cuda=false>
+static inline C10_HOST_DEVICE T chebyshev_polynomial_u_forward(T x, T n) {
+    return chebyshev_polynomial_u_forward(x, static_cast<std::int64_t>(n));
+} // chebyshev_polynomial_u_forward(T x, T n)
 
 C10_CLANG_DIAGNOSTIC_POP()

aten/src/ATen/native/cpu/BinaryOpsKernel.cpp

@@ -1116,7 +1116,15 @@ void chebyshev_polynomial_t_kernel(TensorIteratorBase& iterator) {
             return chebyshev_polynomial_t_forward(x, n);
         });
     });
-}
+} // chebyshev_polynomial_t_kernel(TensorIteratorBase& iterator)
+
+void chebyshev_polynomial_u_kernel(TensorIteratorBase& iterator) {
+    AT_DISPATCH_FLOATING_TYPES(iterator.common_dtype(), "chebyshev_polynomial_u_cpu", [&]() {
+        cpu_kernel(iterator, [](scalar_t x, scalar_t n) -> scalar_t {
+            return chebyshev_polynomial_u_forward(x, n);
+        });
+    });
+} // chebyshev_polynomial_u_kernel(TensorIteratorBase& iterator)
 
 } // namespace
 
@@ -1166,6 +1174,7 @@ REGISTER_DISPATCH(xlogy_stub, &xlogy_kernel);
 REGISTER_DISPATCH(xlog1py_stub, &xlog1py_kernel);
 REGISTER_DISPATCH(zeta_stub, &zeta_kernel);
 REGISTER_DISPATCH(chebyshev_polynomial_t_stub, &chebyshev_polynomial_t_kernel);
+REGISTER_DISPATCH(chebyshev_polynomial_u_stub, &chebyshev_polynomial_u_kernel);
 
 } // namespace native
 } // namespace at

aten/src/ATen/native/cuda/Math.cuh

@@ -1303,13 +1303,63 @@ const auto chebyshev_polynomial_t_string = jiterator_stringify(
         }
 
         return r;
-    }
+    } // chebyshev_polynomial_t_forward(T x, int64_t n)
 
     template<typename T>
     T chebyshev_polynomial_t_forward(T x, T n) {
         return chebyshev_polynomial_t_forward(x, static_cast<int64_t>(n));
-    }
-);
+    } // chebyshev_polynomial_t_forward(T x, T n)
+); // chebyshev_polynomial_t_string
+
+const auto chebyshev_polynomial_u_string = jiterator_stringify(
+    template<typename T>
+    T chebyshev_polynomial_u_forward(T x, int64_t n) {
+        if (n < 0) {
+            return T(0.0);
+        }
+
+        if (abs(x) == T(1.0)) {
+            if (x > T(0.0) || n % 2 == 0) {
+                return n + 1;
+            }
+
+            return -(n + 1);
+        }
+
+        if ((n > 8) && (abs(x) < T(1.0))) {
+            if (sin(acos(x)) != T(0.0)) {
+                return sin((n + 1) * acos(x)) / sin(acos(x));
+            }
+
+            return (n + 1) * cos((n + 1) * acos(x)) / x;
+        }
+
+        if (n == 0) {
+            return T(1.0);
+        }
+
+        if (n == 1) {
+            return x + x;
+        }
+
+        T p = T(1.0);
+        T q = x + x;
+        T r;
+
+        for (int64_t k = 2; k <= n; k++) {
+            r = (x + x) * q - p;
+            p = q;
+            q = r;
+        }
+
+        return r;
+    } // chebyshev_polynomial_u_forward(T x, int64_t n)
+
+    template<typename T>
+    T chebyshev_polynomial_u_forward(T x, T n) {
+        return chebyshev_polynomial_u_forward(x, static_cast<int64_t>(n));
+    } // chebyshev_polynomial_u_forward(T x, T n)
+); // chebyshev_polynomial_u_string
 
 #else // !AT_USE_JITERATOR() -- kernels must be precompiled
 

aten/src/ATen/native/cuda/chebyshev_polynomial_u.cu

@@ -0,0 +1,33 @@
+#define TORCH_ASSERT_NO_OPERATORS
+
+#include <ATen/Dispatch.h>
+#include <ATen/native/cuda/JitLoops.cuh>
+#include <ATen/native/cuda/Loops.cuh>
+#include <ATen/native/BinaryOps.h>
+#include <ATen/native/Math.h>
+#include <ATen/native/cuda/Math.cuh>
+#include <ATen/native/cuda/jit_utils.h>
+
+namespace at {
+    namespace native {
+        namespace {
+            const char chebyshev_polynomial_u_name[] = "chebyshev_polynomial_u_forward";
+
+            void chebyshev_polynomial_u_kernel_cuda(TensorIteratorBase& iterator) {
+#if AT_USE_JITERATOR()
+                AT_DISPATCH_FLOATING_TYPES(iterator.common_dtype(), "chebyshev_polynomial_u_cuda", [&]() {
+                    opmath_jitted_gpu_kernel_with_scalars<chebyshev_polynomial_u_name, scalar_t, scalar_t>(iterator, chebyshev_polynomial_u_string);
+                });
+#else
+                AT_DISPATCH_FLOATING_TYPES(iterator.common_dtype(), "chebyshev_polynomial_u_cuda", [&]() {
+                    gpu_kernel_with_scalars(iterator, []GPU_LAMBDA(scalar_t x, scalar_t n) -> scalar_t {
+                        return chebyshev_polynomial_u_forward<scalar_t, true>(x, n);
+                    });
+                });
+#endif
+            } // chebyshev_polynomial_u_kernel_cuda
+        } // namespace (anonymous)
+
+        REGISTER_DISPATCH(chebyshev_polynomial_u_stub, &chebyshev_polynomial_u_kernel_cuda);
+    } // namespace native
+} // namespace at

aten/src/ATen/native/native_functions.yaml

@@ -12438,3 +12438,40 @@
   device_check: NoCheck
   python_module: special
   variants: function
+
+- func: special_chebyshev_polynomial_u(Tensor x, Tensor n) -> Tensor
+  device_check: NoCheck
+  python_module: special
+  structured_delegate: special_chebyshev_polynomial_u.out
+  variants: function
+
+- func: special_chebyshev_polynomial_u.x_scalar(Scalar x, Tensor n) -> Tensor
+  device_check: NoCheck
+  python_module: special
+  variants: function
+
+- func: special_chebyshev_polynomial_u.n_scalar(Tensor x, Scalar n) -> Tensor
+  device_check: NoCheck
+  python_module: special
+  variants: function
+
+- func: special_chebyshev_polynomial_u.out(Tensor x, Tensor n, *, Tensor(a!) out) -> Tensor(a!)
+  device_check: NoCheck
+  dispatch:
+    CPU, CUDA: special_chebyshev_polynomial_u_out
+  python_module: special
+  structured_inherits: TensorIteratorBase
+  structured: True
+  variants: function
+
+- func: special_chebyshev_polynomial_u.x_scalar_out(Scalar x, Tensor n, *, Tensor(a!) out) -> Tensor(a!)
+  device_check: NoCheck
+  python_module: special
+  variants: function
+
+- func: special_chebyshev_polynomial_u.n_scalar_out(Tensor x, Scalar n, *, Tensor(a!) out) -> Tensor(a!)
+  dispatch:
+    CompositeExplicitAutograd: special_chebyshev_polynomial_u_out
+  device_check: NoCheck
+  python_module: special
+  variants: function

test/allowlist_for_publicAPI.json

@@ -3080,6 +3080,7 @@
   ],
   "torch.special": [
     "chebyshev_polynomial_t",
+    "chebyshev_polynomial_u",
     "digamma",
     "entr",
     "erf",

tools/autograd/derivatives.yaml

@@ -2766,3 +2766,13 @@
 
 - name: special_chebyshev_polynomial_t.n_scalar(Tensor x, Scalar n) -> Tensor
   x: non_differentiable
+
+- name: special_chebyshev_polynomial_u(Tensor x, Tensor n) -> Tensor
+  x: non_differentiable
+  n: non_differentiable
+
+- name: special_chebyshev_polynomial_u.x_scalar(Scalar x, Tensor n) -> Tensor
+  n: non_differentiable
+
+- name: special_chebyshev_polynomial_u.n_scalar(Tensor x, Scalar n) -> Tensor
+  x: non_differentiable

torch/csrc/api/include/torch/special.h

@@ -601,4 +601,40 @@ inline Tensor& chebyshev_polynomial_t_out(Tensor& output, const Tensor& x, const
   return torch::special_chebyshev_polynomial_t_out(output, x, n);
 }
 
+/// Chebyshev polynomial of the second kind.
+///
+/// See https://pytorch.org/docs/master/special.html#torch.special.chebyshev_polynomial_u.
+///
+/// Example:
+///
+/// ```
+/// auto x = torch::randn(128, dtype=kDouble);
+/// auto n = torch::randn(128, dtype=kDouble);
+///
+/// torch::special::chebyshev_polynomial_u(x, n);
+/// ```
+inline Tensor chebyshev_polynomial_u(const Tensor& x, const Tensor& n) {
+  return torch::special_chebyshev_polynomial_u(x, n);
+}
+
+inline Tensor chebyshev_polynomial_u(const Scalar& x, const Tensor& n) {
+  return torch::special_chebyshev_polynomial_u(x, n);
+}
+
+inline Tensor chebyshev_polynomial_u(const Tensor& x, const Scalar& n) {
+  return torch::special_chebyshev_polynomial_u(x, n);
+}
+
+inline Tensor& chebyshev_polynomial_u_out(Tensor& output, const Tensor& x, const Tensor& n) {
+  return torch::special_chebyshev_polynomial_u_out(output, x, n);
+}
+
+inline Tensor& chebyshev_polynomial_u_out(Tensor& output, const Scalar& x, const Tensor& n) {
+  return torch::special_chebyshev_polynomial_u_out(output, x, n);
+}
+
+inline Tensor& chebyshev_polynomial_u_out(Tensor& output, const Tensor& x, const Scalar& n) {
+  return torch::special_chebyshev_polynomial_u_out(output, x, n);
+}
+
 }} // torch::special

torch/overrides.py

@@ -987,6 +987,7 @@ def get_testing_overrides() -> Dict[Callable, Callable]:
         torch.swapaxes: lambda input, dim0, dim1: -1,
         torch.swapdims: lambda input, axis0, axis1: -1,
         torch.special.chebyshev_polynomial_t: lambda input, n, out=None: -1,
+        torch.special.chebyshev_polynomial_u: lambda input, n, out=None: -1,
         torch.special.digamma: lambda input: -1,
         torch.special.entr: lambda input: -1,
         torch.special.erf: lambda input: -1,

torch/special/__init__.py

@@ -4,6 +4,7 @@ from torch._torch_docs import common_args, multi_dim_common
 
 __all__ = [
     'chebyshev_polynomial_t',
+    'chebyshev_polynomial_u',
     'digamma',
     'entr',
     'erf',
@@ -878,3 +879,30 @@ Args:
 Keyword args:
     {out}
 """.format(**common_args))
+
+chebyshev_polynomial_u = _add_docstr(_special.special_chebyshev_polynomial_u,
+                                     r"""
+chebyshev_polynomial_t(input, n, *, out=None) -> Tensor
+
+Chebyshev polynomial of the second kind :math:`U_{n}(\text{input})`.
+
+If :math:`n = 0`, :math:`1` is returned. If :math:`n = 1`,
+:math:`2 \times \text{input}` is returned. If :math:`n < 6` or
+:math:`|\text{input}| > 1`, the recursion:
+
+.. math::
+    T_{n + 1}(\text{input}) = 2 \times \text{input} \times T_{n}(\text{input}) - T_{n - 1}(\text{input})
+
+is evaluated. Otherwise, the explicit trigonometric formula:
+
+.. math::
+    \frac{\text{sin}((n + 1) \times \text{arccos}(\text{input}))}{\text{sin}(\text{arccos}(\text{input}))}
+
+is evaluated.
+
+""" + r"""
+Args:
+    {input}
+Keyword args:
+    {out}
+""".format(**common_args))

torch/testing/_internal/common_methods_invocations.py

@@ -18998,6 +18998,17 @@ op_db: List[OpInfo] = [
         supports_one_python_scalar=True,
         supports_autograd=False,
     ),
+    BinaryUfuncInfo(
+        'special.chebyshev_polynomial_u',
+        dtypes=all_types_and(torch.bool),
+        promotes_int_to_float=True,
+        skips=(
+            DecorateInfo(unittest.skip("Skipped!"), 'TestCudaFuserOpInfo'),
+            DecorateInfo(unittest.skip("Skipped!"), 'TestNNCOpInfo'),
+        ),
+        supports_one_python_scalar=True,
+        supports_autograd=False,
+    ),
 ]
 
 # NOTE [Python References]