ergre

r

Content.md

@@ -33,5 +33,5 @@
 ### 4.深度学习NLP
 ### 5.用序列翻译网络和注意的顺序
 
-## 第六章：PyTorch之生成对抗网络
+## 第六章：PyTorch之深度卷积对抗生成网络
 ## 第七章：PyTorch之强化学习

SeventhSection/ReinforcementLearning.md

@@ -0,0 +1,385 @@
+# 强化学习（DQN）教程
+本教程介绍如何使用PyTorch从[OpenAI Gym](https://gym.openai.com/)中的 CartPole-v0 任务上训练一个Deep Q Learning (DQN) 代理。
+
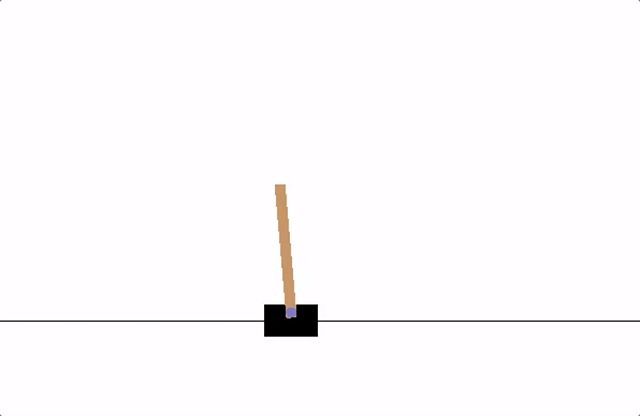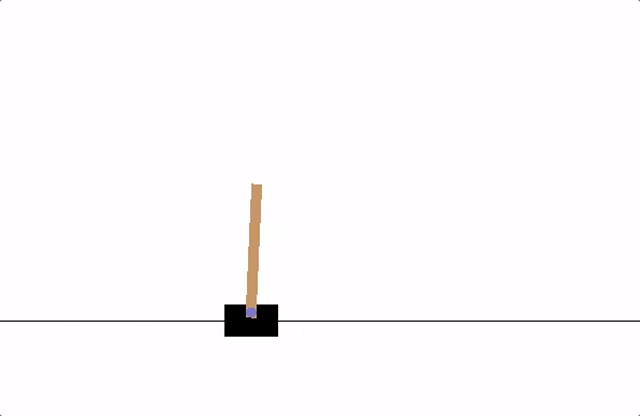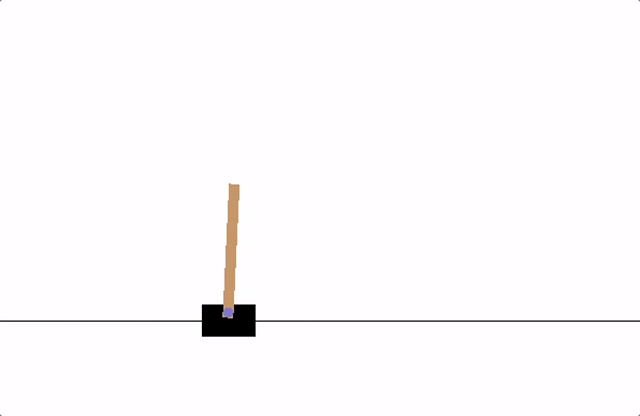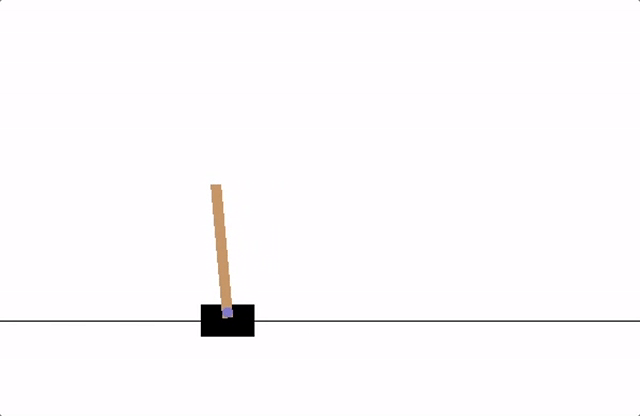
+## 1.任务
+
+代理人必须在两个动作之间做出决定 - 向左或向右移动推车 - 以使连接到它的杆保持直立。您可以在[Gym](https://gym.openai.com/envs/CartPole-v0)
+网站上找到官方排行榜，里面包含各种算法以及可视化。
+
+![](https://pytorch.org/tutorials/_images/cartpole1.gif)
+
+当代理观察环境的当前状态并选择动作时，环境转换到新状态，并且还返回指示动作的后果的奖励。在此任务中，每增加一个时间步长的
+奖励为+1，如果杆落得太远或者推车距离中心超过2.4个单位，则环境终止。这意味着更好的表现场景将持续更长的时间，以及积累更大的回报。
+
+CartPole任务的设计使得代理的输入是4个实际值，表示环境状态（位置，速度等）。然而，神经网络可以纯粹通过观察场景来解决任务，
+因此我们将使用以cart为中心的屏幕补丁作为输入。也因为如此，我们的结果与官方排行榜的结果无法直接比较 - 因为我们的任务
+要困难得多。而且不幸的是，这确实减慢了训练速度，因为我们必须渲染所有帧。
+
+严格地说，我们将状态显示为当前屏幕补丁与前一个补丁之间的差异。这将允许代理从一个图像中考虑杆的速度。
+
+## 2.需要的包
+
+首先，让我们导入所需的包。首先，我们需要[gym](https://gym.openai.com/docs)来得到环境（使用`pip install gym`）。我们还将
+使用PyTorch中的以下内容：
+
+* 神经网络(`torch.nn`)<br/>
+* 优化(`torch.optim`)<br/>
+* 自动分化（`torch.autograd`）<br/>
+* 视觉任务的实用程序(`torchvision`)- 一个单独的包![](https://github.com/pytorch/vision)<br/>
+
+```buildoutcfg
+import gym
+import math
+import random
+import numpy as np
+import matplotlib
+import matplotlib.pyplot as plt
+from collections import namedtuple
+from itertools import count
+from PIL import Image
+
+import torch
+import torch.nn as nn
+import torch.optim as optim
+import torch.nn.functional as F
+import torchvision.transforms as T
+
+
+env = gym.make('CartPole-v0').unwrapped
+
+# set up matplotlib
+is_ipython = 'inline' in matplotlib.get_backend()
+if is_ipython:
+    from IPython import display
+
+plt.ion()
+
+# if gpu is to be used
+device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
+```
+
+## 3. 复现记忆（Replay Memory）
+我们将使用经验重播记忆来训练我们的DQN。它存储代理观察到的转换，允许我们之后重用此数据。通过随机抽样，转换构建相关的一个批次。
+已经表明经验重播记忆极大地稳定并改善了DQN训练程序。
+
+为此，我们需要两个阶段：
+* `Transition`：一个命名元组，表示我们环境中的单个转换。它实际上将（状态，动作）对映射到它们的（next_state，reward）结果，
+状态是屏幕差异图像，如稍后所述<br/>
+* `ReplayMemory`：有界大小的循环缓冲区，用于保存最近观察到的过渡。它还实现了一个`.sample()`方法，用于为训练选择随机batch
+的转换。
+
+```buildoutcfg
+Transition = namedtuple('Transition',
+                        ('state', 'action', 'next_state', 'reward'))
+
+
+class ReplayMemory(object):
+
+    def __init__(self, capacity):
+        self.capacity = capacity
+        self.memory = []
+        self.position = 0
+
+    def push(self, *args):
+        """Saves a transition."""
+        if len(self.memory) < self.capacity:
+            self.memory.append(None)
+        self.memory[self.position] = Transition(*args)
+        self.position = (self.position + 1) % self.capacity
+
+    def sample(self, batch_size):
+        return random.sample(self.memory, batch_size)
+
+    def __len__(self):
+        return len(self.memory)
+```
+
+现在，让我们定义我们的模型。但首先，让我们快速回顾一下DQN是什么。
+
+## 4. DQN 算法
+我们的环境是确定性的，因此为了简单起见，这里给出的所有方程式也是确定性的。在强化学习文献中，它们还包含对环境中随机转变的
+期望。
+
+我们的目标是训练出一种政策，试图最大化折现累积奖励![](notation/公式1.PNG)，其中![](notation/R_t0.gif)也称为回报。折扣![](notation/gamma.gif)
+应该是介于0和1之间的常数，以确保总和收敛。对于我们的代理来说，对比不确定的远期未来，它更看重它们相当有信心的不久的将来。
+
+Q-learning背后的主要思想是，如果我们有一个函数![](notation/公式2.PNG)，它可以告诉我们的回报是什么，如果我们要在给定状态下
+采取行动，那么我们可以轻松地构建最大化我们奖励的政策：
+
+![](notation/公式3.PNG)
+
+但是，我们不了解世界的一切，因此我们无法访问![](notation/Q_.gif)。但是，由于神经网络是通用函数逼近器，我们可以简单地创建
+一个并训练从而使得它类似于![](notation/Q_.gif)。
+
+对于我们的训练更新规则，我们将使用一个事实，即某些策略的每个![](notation/Q.gif)函数都服从 Bellman 方程：
+
+![](notation/公式4.PNG)
+
+平等的两边之间的差异被称为时间差异误差,![](notation/delta.gif):
+
+![](notation/公式5.PNG)
+
+为了最大限度地降低此错误，我们将使用[Huber损失](https://en.wikipedia.org/wiki/Huber_loss)。当误差很小时，Huber损失就像均
+方误差一样，但是当误差很大时，就像平均绝对误差一样 - 当![](notation/Q.gif)的估计噪声很多时，这使得它对异常值更加鲁棒。
+我们通过从重放内存中采样的一批转换![](notation/B.gif)来计算：
+
+![](notation/公式6.PNG)
+
+## 5. Q_网络（Q_network）
+我们的模型将是一个卷积神经网络，它接收当前和之前的屏幕补丁之间的差异。它有两个输出，分别代表![](notation/Q_s_left.gif)和
+![](notation/Q_s_right.gif)（其中s是网络的输入）。实际上，网络正在尝试预测在给定当前输入的情况下采取每个动作的预期回报。
+
+```buildoutcfg
+class DQN(nn.Module):
+
+    def __init__(self, h, w, outputs):
+        super(DQN, self).__init__()
+        self.conv1 = nn.Conv2d(3, 16, kernel_size=5, stride=2)
+        self.bn1 = nn.BatchNorm2d(16)
+        self.conv2 = nn.Conv2d(16, 32, kernel_size=5, stride=2)
+        self.bn2 = nn.BatchNorm2d(32)
+        self.conv3 = nn.Conv2d(32, 32, kernel_size=5, stride=2)
+        self.bn3 = nn.BatchNorm2d(32)
+
+        # 线性输入连接的数量取决于conv2d层的输出，因此取决于输入图像的大小，因此请对其进行计算。
+        def conv2d_size_out(size, kernel_size = 5, stride = 2):
+            return (size - (kernel_size - 1) - 1) // stride  + 1
+        convw = conv2d_size_out(conv2d_size_out(conv2d_size_out(w)))
+        convh = conv2d_size_out(conv2d_size_out(conv2d_size_out(h)))
+        linear_input_size = convw * convh * 32
+        self.head = nn.Linear(linear_input_size, outputs)
+
+    # 使用一个元素调用以确定下一个操作，或在优化期间调用batch。返回tensor([[left0exp,right0exp]...]).
+    def forward(self, x):
+        x = F.relu(self.bn1(self.conv1(x)))
+        x = F.relu(self.bn2(self.conv2(x)))
+        x = F.relu(self.bn3(self.conv3(x)))
+        return self.head(x.view(x.size(0), -1))
+```
+
+## 6. 输入提取
+下面的代码是用于从环境中提取和处理渲染图像的实用程序。它使用了`torchvision`软件包，可以轻松构成图像变换。运行单元后，它将
+显示一个提取的示例补丁。
+
+```buildoutcfg
+resize = T.Compose([T.ToPILImage(),
+                    T.Resize(40, interpolation=Image.CUBIC),
+                    T.ToTensor()])
+
+
+def get_cart_location(screen_width):
+    world_width = env.x_threshold * 2
+    scale = screen_width / world_width
+    return int(env.state[0] * scale + screen_width / 2.0)  # MIDDLE OF CART
+
+def get_screen():
+    # gym要求的返回屏幕是400x600x3，但有时更大，如800x1200x3。 将其转换为torch order（CHW）。
+    screen = env.render(mode='rgb_array').transpose((2, 0, 1))
+    # cart位于下半部分，因此不包括屏幕的顶部和底部
+    _, screen_height, screen_width = screen.shape
+    screen = screen[:, int(screen_height*0.4):int(screen_height * 0.8)]
+    view_width = int(screen_width * 0.6)
+    cart_location = get_cart_location(screen_width)
+    if cart_location < view_width // 2:
+        slice_range = slice(view_width)
+    elif cart_location > (screen_width - view_width // 2):
+        slice_range = slice(-view_width, None)
+    else:
+        slice_range = slice(cart_location - view_width // 2,
+                            cart_location + view_width // 2)
+    # 去掉边缘，使得我们有一个以cart为中心的方形图像
+    screen = screen[:, :, slice_range]
+    # 转换为float类型，重新缩放，转换为torch张量
+    # (this doesn't require a copy)
+    screen = np.ascontiguousarray(screen, dtype=np.float32) / 255
+    screen = torch.from_numpy(screen)
+    # 调整大小并添加batch维度（BCHW）
+    return resize(screen).unsqueeze(0).to(device)
+
+
+env.reset()
+plt.figure()
+plt.imshow(get_screen().cpu().squeeze(0).permute(1, 2, 0).numpy(),
+           interpolation='none')
+plt.title('Example extracted screen')
+plt.show()
+```
+
+## 7. 训练
+#### 7.1 超参数和实用程序
+这个单元实例化我们的模型及其优化器，并定义了一些实用程序：
+* `select_action`：将根据epsilon贪婪政策选择一项行动。简而言之，我们有时会使用我们的模型来选择动作，有时我们只会统一采样。
+选择随机操作的概率将从`EPS_START`开始，并将以指数方式向`EPS_END`衰减。`EPS_DECAY`控制衰减的速度<br/>
+* `plot_durations`：帮助绘制episodes的持续时间，以及过去100个episodes的平均值（官方评估中使用的度量）。该图将位于包含主
+要训练循环的单元下方，并将在每个episodes后更新。<br/>
+
+```buildoutcfg
+BATCH_SIZE = 128
+GAMMA = 0.999
+EPS_START = 0.9
+EPS_END = 0.05
+EPS_DECAY = 200
+TARGET_UPDATE = 10
+
+# 获取屏幕大小，以便我们可以根据AI gym返回的形状正确初始化图层。 
+# 此时的典型尺寸接近3x40x90
+# 这是get_screen（）中的限幅和缩小渲染缓冲区的结果
+init_screen = get_screen()
+_, _, screen_height, screen_width = init_screen.shape
+
+# 从gym行动空间中获取行动数量
+n_actions = env.action_space.n
+
+policy_net = DQN(screen_height, screen_width, n_actions).to(device)
+target_net = DQN(screen_height, screen_width, n_actions).to(device)
+target_net.load_state_dict(policy_net.state_dict())
+target_net.eval()
+
+optimizer = optim.RMSprop(policy_net.parameters())
+memory = ReplayMemory(10000)
+
+
+steps_done = 0
+
+
+def select_action(state):
+    global steps_done
+    sample = random.random()
+    eps_threshold = EPS_END + (EPS_START - EPS_END) * \
+        math.exp(-1. * steps_done / EPS_DECAY)
+    steps_done += 1
+    if sample > eps_threshold:
+        with torch.no_grad():
+            # t.max(1)将返回每行的最大列值。 
+            # 最大结果的第二列是找到最大元素的索引，因此我们选择具有较大预期奖励的行动。
+            return policy_net(state).max(1)[1].view(1, 1)
+    else:
+        return torch.tensor([[random.randrange(n_actions)]], device=device, dtype=torch.long)
+
+
+episode_durations = []
+
+
+def plot_durations():
+    plt.figure(2)
+    plt.clf()
+    durations_t = torch.tensor(episode_durations, dtype=torch.float)
+    plt.title('Training...')
+    plt.xlabel('Episode')
+    plt.ylabel('Duration')
+    plt.plot(durations_t.numpy())
+    # 取100个episode的平均值并绘制它们
+    if len(durations_t) >= 100:
+        means = durations_t.unfold(0, 100, 1).mean(1).view(-1)
+        means = torch.cat((torch.zeros(99), means))
+        plt.plot(means.numpy())
+
+    plt.pause(0.001)  # 暂停一下，以便更新图表
+    if is_ipython:
+        display.clear_output(wait=True)
+        display.display(plt.gcf())
+```
+
+## 8. 训练循环
+在这里，您可以找到执行优化的单个步骤的`optimize_model`函数。它首先对一个batch进行采样，将所有张量连接成一个整体，计算![](notation/Q_sa.gif)
+和![](notation/V()=.gif)，并将它们组合成我们的损失。通过定义，如果s是终端状态，则设置![](notation/V(s)=0.gif)。我们还使
+用目标网络来计算![](notation/V_st+1.gif)以增加稳定性。目标网络的权重在大多数时间保持冻结状态，但每隔一段时间就会更新策略
+网络的权重。这通常是一系列步骤，但为了简单起见，我们将使用episodes。
+
+```buildoutcfg
+def optimize_model():
+    if len(memory) < BATCH_SIZE:
+        return
+    transitions = memory.sample(BATCH_SIZE)
+    # 转置batch（有关详细说明，请参阅https://stackoverflow.com/a/19343/3343043）。
+    # 这会将过渡的batch数组转换为batch数组的过渡。
+    batch = Transition(*zip(*transitions))
+
+    # 计算非最终状态的掩码并连接batch元素（最终状态将是模拟结束后的状态）
+    non_final_mask = torch.tensor(tuple(map(lambda s: s is not None,
+                                          batch.next_state)), device=device, dtype=torch.uint8)
+    non_final_next_states = torch.cat([s for s in batch.next_state
+                                                if s is not None])
+    state_batch = torch.cat(batch.state)
+    action_batch = torch.cat(batch.action)
+    reward_batch = torch.cat(batch.reward)
+
+    # 计算Q(s_t，a) - 模型计算Q(s_t)，然后我们选择所采取的动作列。
+    # 这些是根据policy_net对每个batch状态采取的操作
+    state_action_values = policy_net(state_batch).gather(1, action_batch)
+
+    # 计算所有下一个状态的V(s_{t+1})
+    # non_final_next_states的操作的预期值是基于“较旧的”target_net计算的; 
+    # 用max(1)[0]选择最佳奖励。这是基于掩码合并的，这样我们就可以得到预期的状态值，或者在状态是最终的情况下为0。
+    next_state_values = torch.zeros(BATCH_SIZE, device=device)
+    next_state_values[non_final_mask] = target_net(non_final_next_states).max(1)[0].detach()
+    # 计算预期的Q值
+    expected_state_action_values = (next_state_values * GAMMA) + reward_batch
+
+    # 计算Huber损失
+    loss = F.smooth_l1_loss(state_action_values, expected_state_action_values.unsqueeze(1))
+
+    # 优化模型
+    optimizer.zero_grad()
+    loss.backward()
+    for param in policy_net.parameters():
+        param.grad.data.clamp_(-1, 1)
+    optimizer.step()
+```
+
+下面，您可以找到主要的训练循环。在开始时，我们重置环境并初始`state`张量。然后，我们采样一个动作并执行它，观察下一个屏幕和
+奖励（总是1），并优化我们的模型一次。当episode结束时（我们的模型失败），我们重新开始循环。
+
+下面，*num_episodes*设置为小数值。您应该下载笔记本并运行更多的epsiodes，例如300+以进行有意义的持续时间改进。
+
+```buildoutcfg
+num_episodes = 50
+for i_episode in range(num_episodes):
+    # 初始化环境和状态
+    env.reset()
+    last_screen = get_screen()
+    current_screen = get_screen()
+    state = current_screen - last_screen
+    for t in count():
+        # 选择动作并执行
+        action = select_action(state)
+        _, reward, done, _ = env.step(action.item())
+        reward = torch.tensor([reward], device=device)
+
+        # 观察新的状态
+        last_screen = current_screen
+        current_screen = get_screen()
+        if not done:
+            next_state = current_screen - last_screen
+        else:
+            next_state = None
+
+        # 在记忆中存储过渡
+        memory.push(state, action, next_state, reward)
+
+        # 移动到下一个状态
+        state = next_state
+
+        # 执行优化的一个步骤（在目标网络上）
+        optimize_model()
+        if done:
+            episode_durations.append(t + 1)
+            plot_durations()
+            break
+    # 更新目标网络，复制DQN中的所有权重和偏差
+    if i_episode % TARGET_UPDATE == 0:
+        target_net.load_state_dict(policy_net.state_dict())
+
+print('Complete')
+env.render()
+env.close()
+plt.ioff()
+plt.show()
+```
+
+以下是说明整体结果数据流的图表。
+
+![](https://pytorch.org/tutorials/_images/reinforcement_learning_diagram.jpg)
+
+可以随机选择或根据策略选择操作，从gym环境中获取下一步样本。我们将结果记录在重放内存中，并在每次迭代时运行优化步骤。优化从
+重放内存中选择一个随机batch来进行新策略的训练。“较旧的”target_net也用于优化以计算预期的Q值; 它会偶尔更新以保持最新状态。

SixthSection/Dcgan.md

@@ -0,0 +1,747 @@
+#  DCGAN教程
+## 1. 简介
+本教程通过一个例子来对 DCGANs 进行介绍。我们将会训练一个生成对抗网络（GAN）用于在展示了许多真正的名人的图片后产生新的名人。
+这里的大部分代码来自[pytorch/examples](https://github.com/pytorch/examples)中的 dcgan 实现，本文档将对实现进行进行全面
+的介绍，并阐明该模型的工作原理以及为什么如此。但是不需要担心，你并不需要事先了解 GAN，但可能需要花一些事件来推理一下底层
+实际发生的事情。此外，为了有助于节省时间，最好是使用一个GPU，或者两个。让我们从头开始。
+
+## 2. 生成对抗网络（Generative Adversarial Networks）
+####  2.1 什么是 GAN
+GANs是用于 DL （Deep Learning）模型去捕获训练数据分布情况的框架，以此我们可以从同一分布中生成新的数据。GANs是有Ian Goodfellow
+于2014年提出，并且首次在论文[Generative Adversarial Nets](https://papers.nips.cc/paper/5423-generative-adversarial-nets.pdf)中
+描述。它们由两个不同的模型组成，一个是生成器一个是判别器。生成器的工作是产生看起来像训练图像的“假”图像；判别器的工作是
+查看图像并输出它是否是真实的训练图像或来自生成器的伪图像。在训练期间，产生器不断尝试通过产生越来越好的假动作来超越判别器，
+而判别器则是为了更好地检测并准确地对真实和假图像进行分类。这个游戏的平衡是当生成器产生完美的假动作以使假图像看起来像是来自
+训练数据，而判别器总是猜测生成器输出图像为真或假的概率为50%。
+
+现在，我们开始定义在这个教程中使用到的一些符号。
+
+* 判别器的符号定义
+
+设![](notation/x.gif)表示代表一张图像的数据，![](notation/D(x).gif)
+是判别器网络，它输出![](notation/x.gif)来自训练数据而不是生成器的（标量）概率。这里，由于我们处理图像，![](notation/D(x).gif)
+的输入是 CHW 大小为3x64x64的图像。直观地，当![](notation/x.gif)来自训练数据时![](notation/D(x).gif)应该是 HIGH ，而当x来
+自生成器时![](notation/D(x).gif)应该是 LOW。![](notation/D(x).gif)也可以被认为是传统的二元分类器。
+
+* 生成器的符号定义
+
+对于生成器的符号，让![](notation/z.gif)是从标准正态分布中采样的潜在空间矢量，![](notation/G(z).gif)表示将潜在向量![](notation/z.gif)
+映射到数据空间的生成器函数，![](notation/G.gif)的目标是估计训练数据来自什么分布（![](notation/p_data.gif)），以便它可以
+根据估计的分布（![](notation/p_g.gif)）生成假样本。
+
+因此，![](notation/D_G(z).gif)是生成器![](notation/G.gif)的输出是真实图像的概率（标量）。正如[Goodfellow](https://papers.nips.cc/paper/5423-generative-adversarial-nets.pdf)
+的论文中所描述的，![](notation/D.gif)和![](notation/G.gif)玩一个极小极大的游戏，其中![](notation/D.gif)试图最大化它正确地
+分类真实数据和假样本![](notation/logD(x).gif)的概率，并且![](notation/G.gif)试图最小化![](notation/D.gif)预测其输出是假的
+概率![](notation/log(1-D(G(x))).gif)。从论文来看，GAN 损失函数是:
+
+![](notation/公式1.PNG)
+
+理论上，这个极小极大游戏的解决方案是![](notation/P_g=P_data.gif)，如果输入的是真实的或假的，则判别器会随机猜测。然而，GAN 
+的收敛理论仍在积极研究中，实际上模型并不总是训练到这一点。
+
+####  2.2 什么是 DCGAN
+DCGAN 是上述 GAN 的直接扩展，区别的是它分别在判别器和生成器中明确地使用了卷积和卷积转置层。它首先是由Radford等人在论文
+[Unsupervised Representation Learning With Deep Convolutional Generative Adversarial Networks](https://arxiv.org/pdf/1511.06434.pdf)
+中提出。判别器由 *strided [convolution](https://pytorch.org/docs/stable/nn.html#torch.nn.Conv2d) layers*、*[batch norm](https://pytorch.org/docs/stable/nn.html#torch.nn.BatchNorm2d) layers* 
+和 *[LeakyReLU](https://pytorch.org/docs/stable/nn.html#torch.nn.LeakyReLU) activations* 组成，它输入 3x64x64 的图像，
+然后输出的是一个代表输入是来自实际数据分布的标量概率。生成器则是由 *[convolutional-transpose](https://pytorch.org/docs/stable/nn.html#torch.nn.ConvTranspose2d) layers*、 *batch norm layers* 
+和 *[ReLU](https://pytorch.org/docs/stable/nn.html#relu) activations* 组成。它的输入是从标准正态分布中绘制的潜在向量![](notation/z.gif)，输出是 3x64x64 的 RGB 图像。*strided conv-transpose layers*
+允许潜在标量转换成具有与图像相同形状的体积。在本文中，作者还提供了一些有关如何设置优化器，如何计算损失函数以及如何初始化
+模型权重的提示，所有这些都将在后面的章节中进行说明。
+
+```buildoutcfg
+from __future__ import print_function
+#%matplotlib inline
+import argparse
+import os
+import random
+import torch
+import torch.nn as nn
+import torch.nn.parallel
+import torch.backends.cudnn as cudnn
+import torch.optim as optim
+import torch.utils.data
+import torchvision.datasets as dset
+import torchvision.transforms as transforms
+import torchvision.utils as vutils
+import numpy as np
+import matplotlib.pyplot as plt
+import matplotlib.animation as animation
+from IPython.display import HTML
+
+# 为再现性设置随机seem
+manualSeed = 999
+#manualSeed = random.randint(1, 10000) # 如果你想要新的结果就是要这段代码
+print("Random Seed: ", manualSeed)
+random.seed(manualSeed)
+torch.manual_seed(manualSeed)
+```
+
+* 输出结果：
+
+```buildoutcfg
+Random Seed:  999
+```
+
+## 3. DCGAN实现过程
+#### 3.1 输入
+让我们定义输入数据去运行我们的教程：
+ * **dataroot**：存放数据集根目录的路径。我们将在下一节中详细讨论数据集
+ * **workers**：使用DataLoader加载数据的工作线程数
+ * **batch_size**：训练中使用的batch大小。在DCGAN论文中batch的大小为128
+ * **image_size**：用于训练的图像的空间大小。此实现默认 64x64。如果需要其他尺寸，则必须改变![](notation/D.gif)和![](notation/G.gif)
+ 的结构。有关详细信息，请参见[此处](https://github.com/pytorch/examples/issues/70)。
+ * **nc**：输入图像中的颜色通道数。对于彩色图像，这是参数设置为3
+ * **nz**：潜在向量的长度
+ * **ngf**：与通过生成器携带的特征图的深度有关
+ * **ndf**：设置通过判别器传播的特征映射的深度
+ * **num_epochs**：要运行的训练的epoch数量。长时间的训练可能会带来更好的结果，但也需要更长的时间
+ * **lr**：学习速率。如DCGAN论文中所述，此数字应为0.0002
+ * **beta1**：适用于Adam优化器的beta1超参数。如论文所述，此数字应为0.5
+ * **ngpu**：可用的GPU数量。如果为0，则代码将以CPU模式运行。如果此数字大于0，它将在该数量的GPU上运行
+ 
+ ```buildoutcfg
+# 数据集的根目录
+dataroot = "data/celeba"
+
+# 加载数据的工作线程数
+workers = 2
+
+# 训练期间的batch大小
+batch_size = 128
+
+# 训练图像的空间大小。所有图像将使用变压器调整为此大小。
+image_size = 64
+
+# 训练图像中的通道数。对于彩色图像，这是3
+nc = 3
+
+# 潜在向量 z 的大小(例如： 生成器输入的大小)
+nz = 100
+
+# 生成器中特征图的大小
+ngf = 64
+
+# 判别器中的特征映射的大小
+ndf = 64
+
+# 训练epochs的大小
+num_epochs = 5
+
+# 优化器的学习速率
+lr = 0.0002
+
+# 适用于Adam优化器的Beta1超级参数
+beta1 = 0.5
+
+# 可用的GPU数量。使用0表示CPU模式。
+ngpu = 1
+```
+
+#### 3.2 数据
+在本教程中，我们将使用[Celeb-A Faces](http://mmlab.ie.cuhk.edu.hk/projects/CelebA.html)数据集，该数据集可以在链接或Google Drive中下载。
+数据集将下载为名为*img_align_celeba.zip*的文件。下载后，创建名为*celeba*的目录并将zip文件解压缩到该目录中。然后，将此笔记中
+的数据对象输入设置为刚刚创建的celeba目录。生成的目录结构应该是：
+
+```buildoutcfg
+/path/to/celeba
+    -> img_align_celeba
+        -> 188242.jpg
+        -> 173822.jpg
+        -> 284702.jpg
+        -> 537394.jpg
+```
+这是一个重要的步骤，因为我们将使用`ImageFolder`数据集类，它要求在数据集的根文件夹中有子目录。现在，我们可以创建数据集，创
+建数据加载器，设置要运行的设备，以及最后可视化一些训练数据。
+
+```buildoutcfg
+# 我们可以按照设置的方式使用图像文件夹数据集。
+# 创建数据集
+dataset = dset.ImageFolder(root=dataroot,
+                           transform=transforms.Compose([
+                               transforms.Resize(image_size),
+                               transforms.CenterCrop(image_size),
+                               transforms.ToTensor(),
+                               transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5)),
+                           ]))
+# 创建加载器
+dataloader = torch.utils.data.DataLoader(dataset, batch_size=batch_size,
+                                         shuffle=True, num_workers=workers)
+
+# 选择我们运行在上面的设备
+device = torch.device("cuda:0" if (torch.cuda.is_available() and ngpu > 0) else "cpu")
+
+# 绘制部分我们的输入图像
+real_batch = next(iter(dataloader))
+plt.figure(figsize=(8,8))
+plt.axis("off")
+plt.title("Training Images")
+plt.imshow(np.transpose(vutils.make_grid(real_batch[0].to(device)[:64], padding=2, normalize=True).cpu(),(1,2,0)))
+```
+
+![](https://pytorch.org/tutorials/_images/sphx_glr_dcgan_faces_tutorial_001.png)
+
+## 3.3 实现
+通过设置输入参数和准备好的数据集，我们现在可以进入真正的实现步骤。我们将从权重初始化策略开始，然后详细讨论生成器，鉴别器，
+损失函数和训练循环。
+
+#### 3.3.1 权重初始化
+在`DCGAN`论文中，作者指出所有模型权重应从正态分布中随机初始化，mean = 0，stdev = 0.02。`weights_init`函数将初始化模型作为
+输入，并重新初始化所有卷积，卷积转置和batch标准化层以满足此标准。初始化后立即将此函数应用于模型。
+
+```buildoutcfg
+# custom weights initialization called on netG and netD
+def weights_init(m):
+    classname = m.__class__.__name__
+    if classname.find('Conv') != -1:
+        nn.init.normal_(m.weight.data, 0.0, 0.02)
+    elif classname.find('BatchNorm') != -1:
+        nn.init.normal_(m.weight.data, 1.0, 0.02)
+        nn.init.constant_(m.bias.data, 0)
+```
+
+#### 3.3.2 生成器
+生成器![](notation/G.gif)用于将潜在空间矢量（![](notation/z.gif)）映射到数据空间。由于我们的数据是图像，因此将![](notation/z.gif)
+转换为数据空间意味着最终创建与训练图像具有相同大小的RGB图像（即3x64x64）。实际上，这是通过一系列跨步的二维卷积转置层实现的，
+每个转换层与二维批量标准层和relu activation进行配对。生成器的输出通过`tanh`函数输入，使其返回到[-1,1]范围的输入数据。值得
+注意的是在转换层之后存在批量范数函数，因为这是DCGAN论文的关键贡献。这些层有助于训练期间的梯度流动。DCGAN论文中的生成器中
+的图像如下所示：
+
+![](https://pytorch.org/tutorials/_images/dcgan_generator.png)
+ 
+> 请注意，我们对输入怎么设置（*nz*，*ngf*和*nc*）会影响代码中的生成器体系结构。*nz* 是![](notation/z.gif)输入向量的长度，
+*ngf*与通过生成器传播的特征图的大小有关，*nc*是输出图像中的通道数（对于RGB图像，设置为3）。下面是生成器的代码。
+
+* 生成器代码
+```buildoutcfg
+# 生成器代码
+class Generator(nn.Module):
+    def __init__(self, ngpu):
+        super(Generator, self).__init__()
+        self.ngpu = ngpu
+        self.main = nn.Sequential(
+            # 输入是Z，进入卷积
+            nn.ConvTranspose2d( nz, ngf * 8, 4, 1, 0, bias=False),
+            nn.BatchNorm2d(ngf * 8),
+            nn.ReLU(True),
+            # state size. (ngf*8) x 4 x 4
+            nn.ConvTranspose2d(ngf * 8, ngf * 4, 4, 2, 1, bias=False),
+            nn.BatchNorm2d(ngf * 4),
+            nn.ReLU(True),
+            # state size. (ngf*4) x 8 x 8
+            nn.ConvTranspose2d( ngf * 4, ngf * 2, 4, 2, 1, bias=False),
+            nn.BatchNorm2d(ngf * 2),
+            nn.ReLU(True),
+            # state size. (ngf*2) x 16 x 16
+            nn.ConvTranspose2d( ngf * 2, ngf, 4, 2, 1, bias=False),
+            nn.BatchNorm2d(ngf),
+            nn.ReLU(True),
+            # state size. (ngf) x 32 x 32
+            nn.ConvTranspose2d( ngf, nc, 4, 2, 1, bias=False),
+            nn.Tanh()
+            # state size. (nc) x 64 x 64
+        )
+
+    def forward(self, input):
+        return self.main(input)
+```
+ 现在，我们可以实例化生成器并应用`weights_init`函数。查看打印的模型以查看生成器对象的结构。
+ 
+ ```buildoutcfg
+# 创建生成器
+netG = Generator(ngpu).to(device)
+
+# 如果需要，管理multi-gpu
+if (device.type == 'cuda') and (ngpu > 1):
+    netG = nn.DataParallel(netG, list(range(ngpu)))
+
+# 应用weights_init函数随机初始化所有权重，mean= 0，stdev = 0.2。
+netG.apply(weights_init)
+
+# 打印模型
+print(netG)
+```
+
+* 输出结果：
+
+```buildoutcfg
+Generator(
+  (main): Sequential(
+    (0): ConvTranspose2d(100, 512, kernel_size=(4, 4), stride=(1, 1), bias=False)
+    (1): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
+    (2): ReLU(inplace=True)
+    (3): ConvTranspose2d(512, 256, kernel_size=(4, 4), stride=(2, 2), padding=(1, 1), bias=False)
+    (4): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
+    (5): ReLU(inplace=True)
+    (6): ConvTranspose2d(256, 128, kernel_size=(4, 4), stride=(2, 2), padding=(1, 1), bias=False)
+    (7): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
+    (8): ReLU(inplace=True)
+    (9): ConvTranspose2d(128, 64, kernel_size=(4, 4), stride=(2, 2), padding=(1, 1), bias=False)
+    (10): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
+    (11): ReLU(inplace=True)
+    (12): ConvTranspose2d(64, 3, kernel_size=(4, 4), stride=(2, 2), padding=(1, 1), bias=False)
+    (13): Tanh()
+  )
+)
+```
+
+#### 3.3.3 判别器
+如上所述，判别器![](notation/D.gif)是二进制分类网络，它将图像作为输入并输出输入图像是真实的标量概率（与假的相反）。这里，
+![](notation/D.gif)采用 3x64x64 的输入图像，通过一系列Conv2d，BatchNorm2d和LeakyReLU层处理它，并通过Sigmoid激活函数输出
+最终概率。如果问题需要，可以使用更多层扩展此体系结构，但使用strided convolution（跨步卷积），BatchNorm和LeakyReLU具有重要
+意义。DCGAN论文提到使用跨步卷积而不是池化到降低采样是一种很好的做法，因为它可以让网络学习自己的池化功能。批量标准和 leaky 
+relu函数也促进良好的梯度流，这对于[](notation/G.gif)和[](notation/D.gif)的学习过程都是至关重要的。
+
+* 判别器代码
+
+```buildoutcfg
+class Discriminator(nn.Module):
+    def __init__(self, ngpu):
+        super(Discriminator, self).__init__()
+        self.ngpu = ngpu
+        self.main = nn.Sequential(
+            # input is (nc) x 64 x 64
+            nn.Conv2d(nc, ndf, 4, 2, 1, bias=False),
+            nn.LeakyReLU(0.2, inplace=True),
+            # state size. (ndf) x 32 x 32
+            nn.Conv2d(ndf, ndf * 2, 4, 2, 1, bias=False),
+            nn.BatchNorm2d(ndf * 2),
+            nn.LeakyReLU(0.2, inplace=True),
+            # state size. (ndf*2) x 16 x 16
+            nn.Conv2d(ndf * 2, ndf * 4, 4, 2, 1, bias=False),
+            nn.BatchNorm2d(ndf * 4),
+            nn.LeakyReLU(0.2, inplace=True),
+            # state size. (ndf*4) x 8 x 8
+            nn.Conv2d(ndf * 4, ndf * 8, 4, 2, 1, bias=False),
+            nn.BatchNorm2d(ndf * 8),
+            nn.LeakyReLU(0.2, inplace=True),
+            # state size. (ndf*8) x 4 x 4
+            nn.Conv2d(ndf * 8, 1, 4, 1, 0, bias=False),
+            nn.Sigmoid()
+        )
+
+    def forward(self, input):
+        return self.main(input)
+```
+
+现在，与生成器一样，我们可以创建判别器，应用`weights_init`函数，并打印模型的结构。
+
+```buildoutcfg
+# 创建判别器
+netD = Discriminator(ngpu).to(device)
+
+# Handle multi-gpu if desired
+if (device.type == 'cuda') and (ngpu > 1):
+    netD = nn.DataParallel(netD, list(range(ngpu)))
+
+# 应用weights_init函数随机初始化所有权重，mean= 0，stdev = 0.2
+netD.apply(weights_init)
+
+# 打印模型
+print(netD)
+```
+
+* 输出结果：
+
+```buildoutcfg
+Discriminator(
+  (main): Sequential(
+    (0): Conv2d(3, 64, kernel_size=(4, 4), stride=(2, 2), padding=(1, 1), bias=False)
+    (1): LeakyReLU(negative_slope=0.2, inplace=True)
+    (2): Conv2d(64, 128, kernel_size=(4, 4), stride=(2, 2), padding=(1, 1), bias=False)
+    (3): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
+    (4): LeakyReLU(negative_slope=0.2, inplace=True)
+    (5): Conv2d(128, 256, kernel_size=(4, 4), stride=(2, 2), padding=(1, 1), bias=False)
+    (6): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
+    (7): LeakyReLU(negative_slope=0.2, inplace=True)
+    (8): Conv2d(256, 512, kernel_size=(4, 4), stride=(2, 2), padding=(1, 1), bias=False)
+    (9): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
+    (10): LeakyReLU(negative_slope=0.2, inplace=True)
+    (11): Conv2d(512, 1, kernel_size=(4, 4), stride=(1, 1), bias=False)
+    (12): Sigmoid()
+  )
+)
+```
+
+#### 3.3.4 损失函数和优化器
+通过![](notation/D.gif)和![](notation/G.gif)设置，我们可以指定他们如何通过损失函数和优化器学习。我们将使用PyTorch中定义的
+二进制交叉熵损失（[BCELoss](https://pytorch.org/docs/stable/nn.html#torch.nn.BCELoss)）函数：
+![](notation/公式2.PNG)
+
+注意该函数如何计算目标函数中的两个对数分量（即![](notation/logD(x).gif)和![](notation/log(1-).gif)。我们可以指定用于输入y
+的BCE方程的哪个部分。这是在即将出现的训练循环中完成的，但重要的是要了解我们如何通过改变y（即GT标签）来选择我们希望计算的组件。
+
+接下来，我们将真实标签定义为1，将假标签定义为0。这些标签将在计算![](notation/D.gif)和![](notation/G.gif)的损失时使用，这
+也是原始 GAN 论文中使用的惯例。最后，我们设置了两个单独的优化器，一个用于![](notation/D.gif)，一个用于![](notation/G.gif)。
+如 DCGAN 论文中所述，两者都是Adam优化器，学习率为0.0002，Beta1 = 0.5。 为了跟踪生成器的学习进度，我们将生成一组固定的潜在
+向量，这些向量是从高斯分布（即`fixed_noise`）中提取的。在训练循环中，我们将周期性地将此`fixed_noise`输入到![](notation/G.gif)
+中，并且在迭代中我们将看到图像形成于噪声之外。
+
+```buildoutcfg
+# 初始化BCELoss函数
+criterion = nn.BCELoss()
+
+# 创建一批潜在的向量，我们将用它来可视化生成器的进程
+fixed_noise = torch.randn(64, nz, 1, 1, device=device)
+
+# 在训练期间建立真假标签的惯例
+real_label = 1
+fake_label = 0
+
+# 为 G 和 D 设置 Adam 优化器
+optimizerD = optim.Adam(netD.parameters(), lr=lr, betas=(beta1, 0.999))
+optimizerG = optim.Adam(netG.parameters(), lr=lr, betas=(beta1, 0.999))
+```
+
+#### 3.3.4 训练
+最后，既然已经定义了 GAN 框架的所有部分，我们就可以对其进行训练了。请注意，训练GAN在某种程度上是一种艺术形式，因为不正确
+的超参数设置会导致对错误的解释很少的模式崩溃，在这里，我们将密切关注Goodfellow的论文中的算法1，同时遵守[ganhacks](https://github.com/soumith/ganhacks)
+中展示的一些最佳实践。也就是说，我们将“为真实和虚假”图像构建不同的 mini-batches ，并且还调整![](notation/G.gif)的目标函
+数以最大化![](notation/log_DGz.gif)。训练分为两个主要部分，第1部分更新判别器，第2部分更新生成器。
+
+#### * 第一部分：训练判别器
+回想一下，训练判别器的目的是最大化将给定输入正确分类为真实或假的概率。就Goodfellow而言，我们希望“通过提升其随机梯度来更
+新判别器”。实际上，我们希望最大化![](notation/log+log(1-).gif)。由于ganhacks的独立 mini-batch 建议，我们将分两步计算。首
+先，我们将从训练集构建一批实际样本，向前通过![](notation/D.gif)，计算损失![](notation/logD(x).gif)，然后计算向后传递的梯
+度。其次，我们将用当前生成器构造一批假样本，通过![](notation/D.gif)向前传递该 batch，计算损失![](notation/log(1-).gif)，
+并通过反向传递累积梯度。现在，随着从全实时和全实时批量累积的梯度，我们称之为Discriminator优化器的一步。
+
+#### * 第一部分：训练判别器
+正如原始论文所述，我们希望通过最小化![](notation/log(1-).gif)来训练生成器，以便产生更好的伪样本。如上所述，Goodfellow 表
+明这不会提供足够的梯度，尤其是在学习过程的早期阶段。作为修复，我们希望最大化![](notation/log_DGz.gif)。在代码中，我们通过
+以下方式实现此目的：使用判别器对第1部分的生成器中的输出进行分类，使用真实标签： GT 标签计算![](notation/G.gif)的损失，
+在向后传递中计算![](notation/G.gif)的梯度，最后使用优化器步骤更新![](notation/G.gif)的参数。使用真实标签作为损失函数的GT
+标签似乎是违反直觉的，但是这允许我们使用 BCELoss的![](notation/log(x).gif)部分（而不是![](notation/log(1-x).gif)部分），
+这正是我们想要。
+
+最后，我们将进行一些统计报告，在每个epoch结束时，我们将通过生成器推送我们的fixed_noise batch，以直观地跟踪![](notation/G.gif)
+训练的进度。训练的统计数据是：
+
+* **Loss_D**：判别器损失计算为所有实际批次和所有假批次的损失总和(![](notation/log+log_DGz.gif))
+* **Loss_G**：计算生成器损失(![](notation/log_DGz.gif))
+* **D(x)**：所有实际批次的判别器的平均输出（整批）。当![](notation/G.gif)变好时这应该从接近1开始，然后理论上收敛到0.5。
+想想为什么会这样。
+* **D(G(z))**：所有假批次的平均判别器输出。第一个数字是在![](notation/D.gif)更新之前，第二个数字是在![](notation/D.gif)
+更新之后。当G变好时，这些数字应该从0开始并收敛到0.5。想想为什么会这样。
+
+> 此步骤可能需要一段时间，具体取决于您运行的epoch数以及是否从数据集中删除了一些数据。
+
+```buildoutcfg
+# Training Loop
+
+# Lists to keep track of progress
+img_list = []
+G_losses = []
+D_losses = []
+iters = 0
+
+print("Starting Training Loop...")
+# For each epoch
+for epoch in range(num_epochs):
+    # 对于数据加载器中的每个batch
+    for i, data in enumerate(dataloader, 0):
+
+        ############################
+        # (1) Update D network: maximize log(D(x)) + log(1 - D(G(z)))
+        ###########################
+        ## Train with all-real batch
+        netD.zero_grad()
+        # Format batch
+        real_cpu = data[0].to(device)
+        b_size = real_cpu.size(0)
+        label = torch.full((b_size,), real_label, device=device)
+        # Forward pass real batch through D
+        output = netD(real_cpu).view(-1)
+        # Calculate loss on all-real batch
+        errD_real = criterion(output, label)
+        # Calculate gradients for D in backward pass
+        errD_real.backward()
+        D_x = output.mean().item()
+
+        ## Train with all-fake batch
+        # Generate batch of latent vectors
+        noise = torch.randn(b_size, nz, 1, 1, device=device)
+        # Generate fake image batch with G
+        fake = netG(noise)
+        label.fill_(fake_label)
+        # Classify all fake batch with D
+        output = netD(fake.detach()).view(-1)
+        # Calculate D's loss on the all-fake batch
+        errD_fake = criterion(output, label)
+        # Calculate the gradients for this batch
+        errD_fake.backward()
+        D_G_z1 = output.mean().item()
+        # Add the gradients from the all-real and all-fake batches
+        errD = errD_real + errD_fake
+        # Update D
+        optimizerD.step()
+
+        ############################
+        # (2) Update G network: maximize log(D(G(z)))
+        ###########################
+        netG.zero_grad()
+        label.fill_(real_label)  # fake labels are real for generator cost
+        # Since we just updated D, perform another forward pass of all-fake batch through D
+        output = netD(fake).view(-1)
+        # Calculate G's loss based on this output
+        errG = criterion(output, label)
+        # Calculate gradients for G
+        errG.backward()
+        D_G_z2 = output.mean().item()
+        # Update G
+        optimizerG.step()
+
+        # Output training stats
+        if i % 50 == 0:
+            print('[%d/%d][%d/%d]\tLoss_D: %.4f\tLoss_G: %.4f\tD(x): %.4f\tD(G(z)): %.4f / %.4f'
+                  % (epoch, num_epochs, i, len(dataloader),
+                     errD.item(), errG.item(), D_x, D_G_z1, D_G_z2))
+
+        # Save Losses for plotting later
+        G_losses.append(errG.item())
+        D_losses.append(errD.item())
+
+        # Check how the generator is doing by saving G's output on fixed_noise
+        if (iters % 500 == 0) or ((epoch == num_epochs-1) and (i == len(dataloader)-1)):
+            with torch.no_grad():
+                fake = netG(fixed_noise).detach().cpu()
+            img_list.append(vutils.make_grid(fake, padding=2, normalize=True))
+
+        iters += 1
+```
+
+* 输出结果：
+
+```buildoutcfg
+Starting Training Loop...
+[0/5][0/1583]   Loss_D: 2.0937  Loss_G: 5.2059  D(x): 0.5704    D(G(z)): 0.6680 / 0.0090
+[0/5][50/1583]  Loss_D: 0.3567  Loss_G: 12.2064 D(x): 0.9364    D(G(z)): 0.1409 / 0.0000
+[0/5][100/1583] Loss_D: 0.3519  Loss_G: 8.8873  D(x): 0.8714    D(G(z)): 0.0327 / 0.0004
+[0/5][150/1583] Loss_D: 0.5300  Loss_G: 6.6410  D(x): 0.8918    D(G(z)): 0.2776 / 0.0030
+[0/5][200/1583] Loss_D: 0.2543  Loss_G: 4.3581  D(x): 0.8662    D(G(z)): 0.0844 / 0.0218
+[0/5][250/1583] Loss_D: 0.7170  Loss_G: 4.2652  D(x): 0.8285    D(G(z)): 0.3227 / 0.0370
+[0/5][300/1583] Loss_D: 0.5739  Loss_G: 4.2060  D(x): 0.8329    D(G(z)): 0.2577 / 0.0305
+[0/5][350/1583] Loss_D: 0.8139  Loss_G: 6.5680  D(x): 0.9163    D(G(z)): 0.3844 / 0.0062
+[0/5][400/1583] Loss_D: 0.4089  Loss_G: 5.0794  D(x): 0.8580    D(G(z)): 0.1221 / 0.0243
+[0/5][450/1583] Loss_D: 0.4785  Loss_G: 4.1612  D(x): 0.7154    D(G(z)): 0.0514 / 0.0258
+[0/5][500/1583] Loss_D: 0.3748  Loss_G: 4.2888  D(x): 0.8135    D(G(z)): 0.0955 / 0.0264
+[0/5][550/1583] Loss_D: 0.5247  Loss_G: 5.9952  D(x): 0.8347    D(G(z)): 0.1580 / 0.0075
+[0/5][600/1583] Loss_D: 0.7765  Loss_G: 2.2662  D(x): 0.5977    D(G(z)): 0.0408 / 0.1708
+[0/5][650/1583] Loss_D: 0.6914  Loss_G: 4.4091  D(x): 0.6502    D(G(z)): 0.0266 / 0.0238
+[0/5][700/1583] Loss_D: 0.5679  Loss_G: 5.3386  D(x): 0.8476    D(G(z)): 0.2810 / 0.0098
+[0/5][750/1583] Loss_D: 0.3717  Loss_G: 5.1295  D(x): 0.9221    D(G(z)): 0.2207 / 0.0106
+[0/5][800/1583] Loss_D: 0.4423  Loss_G: 3.1339  D(x): 0.8418    D(G(z)): 0.1655 / 0.0820
+[0/5][850/1583] Loss_D: 0.3391  Loss_G: 4.8393  D(x): 0.7920    D(G(z)): 0.0315 / 0.0169
+[0/5][900/1583] Loss_D: 0.4346  Loss_G: 4.3887  D(x): 0.8883    D(G(z)): 0.2270 / 0.0202
+[0/5][950/1583] Loss_D: 0.5315  Loss_G: 4.6233  D(x): 0.8393    D(G(z)): 0.2490 / 0.0188
+[0/5][1000/1583]        Loss_D: 0.5281  Loss_G: 6.1465  D(x): 0.9643    D(G(z)): 0.3270 / 0.0049
+[0/5][1050/1583]        Loss_D: 0.5515  Loss_G: 6.4457  D(x): 0.9262    D(G(z)): 0.3361 / 0.0033
+[0/5][1100/1583]        Loss_D: 0.4430  Loss_G: 4.7469  D(x): 0.7306    D(G(z)): 0.0184 / 0.0202
+[0/5][1150/1583]        Loss_D: 0.7336  Loss_G: 2.6978  D(x): 0.6552    D(G(z)): 0.1293 / 0.1059
+[0/5][1200/1583]        Loss_D: 0.2927  Loss_G: 4.7480  D(x): 0.8858    D(G(z)): 0.1329 / 0.0173
+[0/5][1250/1583]        Loss_D: 2.0790  Loss_G: 5.1077  D(x): 0.2722    D(G(z)): 0.0036 / 0.0172
+[0/5][1300/1583]        Loss_D: 0.2431  Loss_G: 5.0027  D(x): 0.8812    D(G(z)): 0.0816 / 0.0169
+[0/5][1350/1583]        Loss_D: 0.2969  Loss_G: 4.6160  D(x): 0.9126    D(G(z)): 0.1609 / 0.0183
+[0/5][1400/1583]        Loss_D: 0.7158  Loss_G: 2.9825  D(x): 0.6117    D(G(z)): 0.0292 / 0.0900
+[0/5][1450/1583]        Loss_D: 0.7513  Loss_G: 1.9396  D(x): 0.6186    D(G(z)): 0.0559 / 0.2414
+[0/5][1500/1583]        Loss_D: 0.4366  Loss_G: 3.9122  D(x): 0.8736    D(G(z)): 0.2231 / 0.0325
+[0/5][1550/1583]        Loss_D: 0.3204  Loss_G: 4.2434  D(x): 0.8395    D(G(z)): 0.0929 / 0.0271
+[1/5][0/1583]   Loss_D: 0.5077  Loss_G: 4.8872  D(x): 0.9331    D(G(z)): 0.3082 / 0.0122
+[1/5][50/1583]  Loss_D: 0.5637  Loss_G: 3.6652  D(x): 0.8525    D(G(z)): 0.2684 / 0.0414
+[1/5][100/1583] Loss_D: 0.4047  Loss_G: 3.6624  D(x): 0.8323    D(G(z)): 0.1508 / 0.0473
+[1/5][150/1583] Loss_D: 0.3858  Loss_G: 3.3070  D(x): 0.7873    D(G(z)): 0.0826 / 0.0583
+[1/5][200/1583] Loss_D: 0.4348  Loss_G: 3.6292  D(x): 0.8390    D(G(z)): 0.1908 / 0.0417
+[1/5][250/1583] Loss_D: 0.5953  Loss_G: 2.1992  D(x): 0.6572    D(G(z)): 0.0649 / 0.1540
+[1/5][300/1583] Loss_D: 0.4062  Loss_G: 3.8770  D(x): 0.8655    D(G(z)): 0.2012 / 0.0310
+[1/5][350/1583] Loss_D: 0.9472  Loss_G: 1.4837  D(x): 0.4979    D(G(z)): 0.0322 / 0.2947
+[1/5][400/1583] Loss_D: 0.5269  Loss_G: 2.6842  D(x): 0.9150    D(G(z)): 0.2922 / 0.1248
+[1/5][450/1583] Loss_D: 0.6091  Loss_G: 3.8100  D(x): 0.8194    D(G(z)): 0.2720 / 0.0360
+[1/5][500/1583] Loss_D: 0.5674  Loss_G: 3.2716  D(x): 0.8279    D(G(z)): 0.2452 / 0.0610
+[1/5][550/1583] Loss_D: 0.8366  Loss_G: 5.5266  D(x): 0.9263    D(G(z)): 0.4840 / 0.0076
+[1/5][600/1583] Loss_D: 0.6098  Loss_G: 2.2626  D(x): 0.6424    D(G(z)): 0.0640 / 0.1451
+[1/5][650/1583] Loss_D: 0.3970  Loss_G: 3.4130  D(x): 0.8347    D(G(z)): 0.1613 / 0.0491
+[1/5][700/1583] Loss_D: 0.5422  Loss_G: 3.1208  D(x): 0.7889    D(G(z)): 0.1972 / 0.0699
+[1/5][750/1583] Loss_D: 0.9114  Loss_G: 1.3789  D(x): 0.5066    D(G(z)): 0.0350 / 0.3440
+[1/5][800/1583] Loss_D: 1.1917  Loss_G: 5.6081  D(x): 0.9548    D(G(z)): 0.6084 / 0.0064
+[1/5][850/1583] Loss_D: 0.4852  Loss_G: 1.9158  D(x): 0.7103    D(G(z)): 0.0636 / 0.1943
+[1/5][900/1583] Loss_D: 0.5322  Loss_G: 2.8350  D(x): 0.7762    D(G(z)): 0.1994 / 0.0868
+[1/5][950/1583] Loss_D: 0.7765  Loss_G: 1.7411  D(x): 0.5553    D(G(z)): 0.0732 / 0.2260
+[1/5][1000/1583]        Loss_D: 0.5518  Loss_G: 4.5488  D(x): 0.9244    D(G(z)): 0.3354 / 0.0161
+[1/5][1050/1583]        Loss_D: 0.4237  Loss_G: 3.2012  D(x): 0.8118    D(G(z)): 0.1651 / 0.0583
+[1/5][1100/1583]        Loss_D: 1.1245  Loss_G: 5.5327  D(x): 0.9483    D(G(z)): 0.5854 / 0.0090
+[1/5][1150/1583]        Loss_D: 0.5543  Loss_G: 1.9609  D(x): 0.6777    D(G(z)): 0.0933 / 0.1936
+[1/5][1200/1583]        Loss_D: 0.4945  Loss_G: 2.0234  D(x): 0.7580    D(G(z)): 0.1329 / 0.1742
+[1/5][1250/1583]        Loss_D: 0.5637  Loss_G: 2.9421  D(x): 0.7701    D(G(z)): 0.2123 / 0.0780
+[1/5][1300/1583]        Loss_D: 0.6178  Loss_G: 2.5512  D(x): 0.7828    D(G(z)): 0.2531 / 0.1068
+[1/5][1350/1583]        Loss_D: 0.4302  Loss_G: 2.5266  D(x): 0.8525    D(G(z)): 0.2053 / 0.1141
+[1/5][1400/1583]        Loss_D: 1.5730  Loss_G: 1.4042  D(x): 0.2854    D(G(z)): 0.0183 / 0.3325
+[1/5][1450/1583]        Loss_D: 0.6962  Loss_G: 3.3562  D(x): 0.8652    D(G(z)): 0.3732 / 0.0534
+[1/5][1500/1583]        Loss_D: 0.7635  Loss_G: 1.4343  D(x): 0.5765    D(G(z)): 0.0807 / 0.3056
+[1/5][1550/1583]        Loss_D: 0.4228  Loss_G: 3.3460  D(x): 0.8169    D(G(z)): 0.1671 / 0.0522
+[2/5][0/1583]   Loss_D: 0.8332  Loss_G: 1.5990  D(x): 0.6355    D(G(z)): 0.2409 / 0.2433
+[2/5][50/1583]  Loss_D: 0.4681  Loss_G: 2.0920  D(x): 0.7295    D(G(z)): 0.0978 / 0.1626
+[2/5][100/1583] Loss_D: 0.7995  Loss_G: 2.8227  D(x): 0.7766    D(G(z)): 0.3675 / 0.0828
+[2/5][150/1583] Loss_D: 0.3804  Loss_G: 2.6037  D(x): 0.8523    D(G(z)): 0.1729 / 0.1016
+[2/5][200/1583] Loss_D: 0.9238  Loss_G: 0.8758  D(x): 0.5284    D(G(z)): 0.1343 / 0.4542
+[2/5][250/1583] Loss_D: 0.5205  Loss_G: 2.6795  D(x): 0.7778    D(G(z)): 0.1875 / 0.0934
+[2/5][300/1583] Loss_D: 0.7720  Loss_G: 3.8033  D(x): 0.9307    D(G(z)): 0.4405 / 0.0384
+[2/5][350/1583] Loss_D: 0.5825  Loss_G: 3.3677  D(x): 0.9309    D(G(z)): 0.3609 / 0.0470
+[2/5][400/1583] Loss_D: 0.4290  Loss_G: 2.5963  D(x): 0.7495    D(G(z)): 0.1047 / 0.0976
+[2/5][450/1583] Loss_D: 0.7161  Loss_G: 4.0053  D(x): 0.8270    D(G(z)): 0.3655 / 0.0252
+[2/5][500/1583] Loss_D: 0.5238  Loss_G: 2.3543  D(x): 0.8084    D(G(z)): 0.2320 / 0.1330
+[2/5][550/1583] Loss_D: 0.7724  Loss_G: 2.2096  D(x): 0.6645    D(G(z)): 0.2238 / 0.1417
+[2/5][600/1583] Loss_D: 0.4897  Loss_G: 2.8286  D(x): 0.7776    D(G(z)): 0.1738 / 0.0832
+[2/5][650/1583] Loss_D: 1.2680  Loss_G: 4.7502  D(x): 0.8977    D(G(z)): 0.6179 / 0.0149
+[2/5][700/1583] Loss_D: 0.7054  Loss_G: 3.3908  D(x): 0.8692    D(G(z)): 0.3753 / 0.0490
+[2/5][750/1583] Loss_D: 0.4933  Loss_G: 3.6839  D(x): 0.8933    D(G(z)): 0.2845 / 0.0368
+[2/5][800/1583] Loss_D: 0.6246  Loss_G: 2.7728  D(x): 0.8081    D(G(z)): 0.2968 / 0.0821
+[2/5][850/1583] Loss_D: 1.2216  Loss_G: 1.1784  D(x): 0.3819    D(G(z)): 0.0446 / 0.3623
+[2/5][900/1583] Loss_D: 0.6578  Loss_G: 1.7445  D(x): 0.6494    D(G(z)): 0.1271 / 0.2173
+[2/5][950/1583] Loss_D: 0.8333  Loss_G: 1.2805  D(x): 0.5193    D(G(z)): 0.0543 / 0.3210
+[2/5][1000/1583]        Loss_D: 0.7348  Loss_G: 0.7953  D(x): 0.5920    D(G(z)): 0.1265 / 0.4815
+[2/5][1050/1583]        Loss_D: 0.6809  Loss_G: 3.7259  D(x): 0.8793    D(G(z)): 0.3686 / 0.0401
+[2/5][1100/1583]        Loss_D: 0.7728  Loss_G: 2.1345  D(x): 0.5886    D(G(z)): 0.1234 / 0.1626
+[2/5][1150/1583]        Loss_D: 0.9383  Loss_G: 3.7146  D(x): 0.8942    D(G(z)): 0.5075 / 0.0355
+[2/5][1200/1583]        Loss_D: 0.4951  Loss_G: 2.8725  D(x): 0.8084    D(G(z)): 0.2163 / 0.0764
+[2/5][1250/1583]        Loss_D: 0.6952  Loss_G: 2.1559  D(x): 0.6769    D(G(z)): 0.2063 / 0.1561
+[2/5][1300/1583]        Loss_D: 0.4560  Loss_G: 2.6873  D(x): 0.7993    D(G(z)): 0.1710 / 0.0908
+[2/5][1350/1583]        Loss_D: 0.9185  Loss_G: 3.9262  D(x): 0.8631    D(G(z)): 0.4938 / 0.0276
+[2/5][1400/1583]        Loss_D: 0.5935  Loss_G: 1.2768  D(x): 0.6625    D(G(z)): 0.1064 / 0.3214
+[2/5][1450/1583]        Loss_D: 0.8836  Loss_G: 4.0820  D(x): 0.9368    D(G(z)): 0.5101 / 0.0251
+[2/5][1500/1583]        Loss_D: 0.5268  Loss_G: 2.1486  D(x): 0.7462    D(G(z)): 0.1701 / 0.1450
+[2/5][1550/1583]        Loss_D: 0.5581  Loss_G: 3.0543  D(x): 0.8082    D(G(z)): 0.2489 / 0.0644
+[3/5][0/1583]   Loss_D: 0.6875  Loss_G: 2.3447  D(x): 0.7796    D(G(z)): 0.3180 / 0.1182
+[3/5][50/1583]  Loss_D: 0.7772  Loss_G: 1.2497  D(x): 0.5569    D(G(z)): 0.0763 / 0.3372
+[3/5][100/1583] Loss_D: 1.8087  Loss_G: 0.8440  D(x): 0.2190    D(G(z)): 0.0213 / 0.4701
+[3/5][150/1583] Loss_D: 0.6292  Loss_G: 2.8794  D(x): 0.8807    D(G(z)): 0.3623 / 0.0741
+[3/5][200/1583] Loss_D: 0.5880  Loss_G: 2.2299  D(x): 0.8279    D(G(z)): 0.3026 / 0.1316
+[3/5][250/1583] Loss_D: 0.7737  Loss_G: 1.2797  D(x): 0.5589    D(G(z)): 0.0836 / 0.3363
+[3/5][300/1583] Loss_D: 0.5120  Loss_G: 1.5623  D(x): 0.7216    D(G(z)): 0.1406 / 0.2430
+[3/5][350/1583] Loss_D: 0.5651  Loss_G: 3.2310  D(x): 0.8586    D(G(z)): 0.3048 / 0.0518
+[3/5][400/1583] Loss_D: 1.3554  Loss_G: 5.0320  D(x): 0.9375    D(G(z)): 0.6663 / 0.0112
+[3/5][450/1583] Loss_D: 0.5939  Loss_G: 1.9385  D(x): 0.6931    D(G(z)): 0.1538 / 0.1785
+[3/5][500/1583] Loss_D: 1.5698  Loss_G: 5.0469  D(x): 0.9289    D(G(z)): 0.7124 / 0.0106
+[3/5][550/1583] Loss_D: 0.5496  Loss_G: 1.7024  D(x): 0.6891    D(G(z)): 0.1171 / 0.2172
+[3/5][600/1583] Loss_D: 2.0152  Loss_G: 6.4814  D(x): 0.9824    D(G(z)): 0.8069 / 0.0031
+[3/5][650/1583] Loss_D: 0.6249  Loss_G: 2.9602  D(x): 0.8547    D(G(z)): 0.3216 / 0.0707
+[3/5][700/1583] Loss_D: 0.4448  Loss_G: 2.3997  D(x): 0.8289    D(G(z)): 0.2034 / 0.1153
+[3/5][750/1583] Loss_D: 0.5768  Loss_G: 2.5956  D(x): 0.8094    D(G(z)): 0.2721 / 0.1032
+[3/5][800/1583] Loss_D: 0.5314  Loss_G: 2.9121  D(x): 0.8603    D(G(z)): 0.2838 / 0.0724
+[3/5][850/1583] Loss_D: 0.9673  Loss_G: 4.2585  D(x): 0.9067    D(G(z)): 0.5233 / 0.0206
+[3/5][900/1583] Loss_D: 0.7076  Loss_G: 2.7892  D(x): 0.7294    D(G(z)): 0.2625 / 0.0909
+[3/5][950/1583] Loss_D: 0.4336  Loss_G: 2.8206  D(x): 0.8736    D(G(z)): 0.2363 / 0.0770
+[3/5][1000/1583]        Loss_D: 0.6914  Loss_G: 1.9334  D(x): 0.6811    D(G(z)): 0.2143 / 0.1734
+[3/5][1050/1583]        Loss_D: 0.6618  Loss_G: 1.8457  D(x): 0.6486    D(G(z)): 0.1421 / 0.2036
+[3/5][1100/1583]        Loss_D: 0.6517  Loss_G: 3.2499  D(x): 0.8540    D(G(z)): 0.3491 / 0.0532
+[3/5][1150/1583]        Loss_D: 0.6688  Loss_G: 3.9172  D(x): 0.9389    D(G(z)): 0.4170 / 0.0269
+[3/5][1200/1583]        Loss_D: 0.9467  Loss_G: 0.8899  D(x): 0.4853    D(G(z)): 0.1028 / 0.4567
+[3/5][1250/1583]        Loss_D: 0.6048  Loss_G: 3.3952  D(x): 0.8353    D(G(z)): 0.3150 / 0.0425
+[3/5][1300/1583]        Loss_D: 0.4915  Loss_G: 2.5383  D(x): 0.7663    D(G(z)): 0.1622 / 0.1071
+[3/5][1350/1583]        Loss_D: 0.7804  Loss_G: 1.5018  D(x): 0.5405    D(G(z)): 0.0719 / 0.2701
+[3/5][1400/1583]        Loss_D: 0.6432  Loss_G: 1.5893  D(x): 0.6069    D(G(z)): 0.0576 / 0.2577
+[3/5][1450/1583]        Loss_D: 0.7720  Loss_G: 3.8510  D(x): 0.9291    D(G(z)): 0.4558 / 0.0299
+[3/5][1500/1583]        Loss_D: 0.9340  Loss_G: 4.6210  D(x): 0.9556    D(G(z)): 0.5341 / 0.0141
+[3/5][1550/1583]        Loss_D: 0.7278  Loss_G: 4.0992  D(x): 0.9071    D(G(z)): 0.4276 / 0.0231
+[4/5][0/1583]   Loss_D: 0.4672  Loss_G: 1.9660  D(x): 0.7085    D(G(z)): 0.0815 / 0.1749
+[4/5][50/1583]  Loss_D: 0.5710  Loss_G: 2.3229  D(x): 0.6559    D(G(z)): 0.0654 / 0.1285
+[4/5][100/1583] Loss_D: 0.8091  Loss_G: 0.8053  D(x): 0.5301    D(G(z)): 0.0609 / 0.4987
+[4/5][150/1583] Loss_D: 0.5661  Loss_G: 1.4238  D(x): 0.6836    D(G(z)): 0.1228 / 0.2842
+[4/5][200/1583] Loss_D: 0.6187  Loss_G: 1.6628  D(x): 0.6178    D(G(z)): 0.0744 / 0.2292
+[4/5][250/1583] Loss_D: 0.9808  Loss_G: 2.0649  D(x): 0.5769    D(G(z)): 0.2623 / 0.1706
+[4/5][300/1583] Loss_D: 0.6530  Loss_G: 2.7874  D(x): 0.8024    D(G(z)): 0.3063 / 0.0804
+[4/5][350/1583] Loss_D: 0.5535  Loss_G: 2.5154  D(x): 0.7744    D(G(z)): 0.2165 / 0.1023
+[4/5][400/1583] Loss_D: 0.5277  Loss_G: 2.1542  D(x): 0.6766    D(G(z)): 0.0801 / 0.1474
+[4/5][450/1583] Loss_D: 0.5995  Loss_G: 2.6477  D(x): 0.7890    D(G(z)): 0.2694 / 0.0902
+[4/5][500/1583] Loss_D: 0.7183  Loss_G: 1.2993  D(x): 0.5748    D(G(z)): 0.1000 / 0.3213
+[4/5][550/1583] Loss_D: 0.4708  Loss_G: 2.0671  D(x): 0.7286    D(G(z)): 0.1094 / 0.1526
+[4/5][600/1583] Loss_D: 0.5865  Loss_G: 1.9083  D(x): 0.7084    D(G(z)): 0.1745 / 0.1867
+[4/5][650/1583] Loss_D: 1.5298  Loss_G: 4.2918  D(x): 0.9623    D(G(z)): 0.7240 / 0.0197
+[4/5][700/1583] Loss_D: 0.9155  Loss_G: 0.9452  D(x): 0.4729    D(G(z)): 0.0575 / 0.4395
+[4/5][750/1583] Loss_D: 0.7500  Loss_G: 1.7498  D(x): 0.5582    D(G(z)): 0.0772 / 0.2095
+[4/5][800/1583] Loss_D: 0.5993  Loss_G: 2.5779  D(x): 0.7108    D(G(z)): 0.1829 / 0.1063
+[4/5][850/1583] Loss_D: 0.6787  Loss_G: 3.6855  D(x): 0.9201    D(G(z)): 0.4084 / 0.0347
+[4/5][900/1583] Loss_D: 1.2792  Loss_G: 2.2909  D(x): 0.6365    D(G(z)): 0.4471 / 0.1575
+[4/5][950/1583] Loss_D: 0.6995  Loss_G: 3.3548  D(x): 0.9201    D(G(z)): 0.4188 / 0.0488
+[4/5][1000/1583]        Loss_D: 0.6913  Loss_G: 3.9969  D(x): 0.8630    D(G(z)): 0.3771 / 0.0242
+[4/5][1050/1583]        Loss_D: 0.7620  Loss_G: 1.7744  D(x): 0.6668    D(G(z)): 0.2290 / 0.2204
+[4/5][1100/1583]        Loss_D: 0.6901  Loss_G: 3.1660  D(x): 0.8472    D(G(z)): 0.3595 / 0.0593
+[4/5][1150/1583]        Loss_D: 0.5866  Loss_G: 2.4580  D(x): 0.7962    D(G(z)): 0.2695 / 0.1049
+[4/5][1200/1583]        Loss_D: 0.8830  Loss_G: 3.9824  D(x): 0.9264    D(G(z)): 0.5007 / 0.0264
+[4/5][1250/1583]        Loss_D: 0.4750  Loss_G: 2.1389  D(x): 0.8004    D(G(z)): 0.1933 / 0.1464
+[4/5][1300/1583]        Loss_D: 0.4972  Loss_G: 2.3561  D(x): 0.8266    D(G(z)): 0.2325 / 0.1285
+[4/5][1350/1583]        Loss_D: 0.6721  Loss_G: 1.1904  D(x): 0.6042    D(G(z)): 0.0839 / 0.3486
+[4/5][1400/1583]        Loss_D: 0.4447  Loss_G: 2.7106  D(x): 0.8540    D(G(z)): 0.2219 / 0.0852
+[4/5][1450/1583]        Loss_D: 0.4864  Loss_G: 2.5237  D(x): 0.7153    D(G(z)): 0.1017 / 0.1036
+[4/5][1500/1583]        Loss_D: 0.7662  Loss_G: 1.1344  D(x): 0.5429    D(G(z)): 0.0600 / 0.3805
+[4/5][1550/1583]        Loss_D: 0.4294  Loss_G: 2.9664  D(x): 0.8335    D(G(z)): 0.1943 / 0.0689
+```
+
+
+#### 3.3.5 结果
+最后，让我们看看我们是如何做到的。在这里，我们将看看三个不同的结果。首先，我们将看到![](notation/D.gif)和![](notation/G.gif)
+的损失在训练期间是如何变化的。其次，我们将可视化在每个epoch的 fixed_noise batch中![](notation/G.gif)的输出。第三，我们将
+查看来自![](notation/G.gif)的紧邻一批实际数据的一批假数据。
+
+#### 损失与训练迭代
+下面是D＆G的损失与训练迭代的关系图。
+
+```buildoutcfg
+plt.figure(figsize=(10,5))
+plt.title("Generator and Discriminator Loss During Training")
+plt.plot(G_losses,label="G")
+plt.plot(D_losses,label="D")
+plt.xlabel("iterations")
+plt.ylabel("Loss")
+plt.legend()
+plt.show()
+```
+
+![](https://pytorch.org/tutorials/_images/sphx_glr_dcgan_faces_tutorial_002.png)
+
+#### G的过程可视化
+记住在每个训练epoch之后我们如何在fixed_noise batch中保存生成器的输出。现在，我们可以通过动画可视化G的训练进度。按播放按钮
+开始动画。
+
+```buildoutcfg
+#%%capture
+fig = plt.figure(figsize=(8,8))
+plt.axis("off")
+ims = [[plt.imshow(np.transpose(i,(1,2,0)), animated=True)] for i in img_list]
+ani = animation.ArtistAnimation(fig, ims, interval=1000, repeat_delay=1000, blit=True)
+
+HTML(ani.to_jshtml())
+```
+
+![](https://pytorch.org/tutorials/_images/sphx_glr_dcgan_faces_tutorial_003.png)
+
+#### 真实图像 vs 伪图像
+最后，让我们一起看看一些真实的图像和伪图像。
+
+```buildoutcfg
+# 从数据加载器中获取一批真实图像
+real_batch = next(iter(dataloader))
+
+# 绘制真实图像
+plt.figure(figsize=(15,15))
+plt.subplot(1,2,1)
+plt.axis("off")
+plt.title("Real Images")
+plt.imshow(np.transpose(vutils.make_grid(real_batch[0].to(device)[:64], padding=5, normalize=True).cpu(),(1,2,0)))
+
+# 在最后一个epoch中绘制伪图像
+plt.subplot(1,2,2)
+plt.axis("off")
+plt.title("Fake Images")
+plt.imshow(np.transpose(img_list[-1],(1,2,0)))
+plt.show()
+```
+
+![](https://pytorch.org/tutorials/_images/sphx_glr_dcgan_faces_tutorial_004.png)
+
+## 进一步的工作
+我们已经完成了我们的整个教程，但是你可以从下面几个方向进一步探讨。 你可以：
+
+* 训练更长时间，看看结果有多好<br/>
+* 修改此模型以获取不同的数据集，并或者更改图像和模型体系结构的大小<br/>
+* 在[这里](https://github.com/nashory/gans-awesome-applications)查看其他一些很酷的GAN项目<br/>
+* 创建生成[音乐](https://github.com/nashory/gans-awesome-applications)的GAN<br/>